1.等效法：

等效方法是在保证某种效果(特性和关系)相同的前提下，将实际的、复杂的物理问题和物理过程转化为等效的、简单的、易于研究的物理问题和物理过程来研究和处理的方法。

新高考的选拔愈来愈注重考生的能力和素质，其命题愈加明显地渗透着物理思想、物理方法的考查，等效思想和方法作为一种迅速解决物理问题的有效手段，仍将体现于高考命题的突破过程中。

图26-2

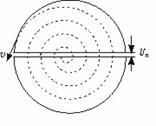
［例1］(★★★★)(物理过程的等效)如图26-2所示，已知回旋加速器中，D形盒内匀强磁场的磁感应强度B = 1.5T ，盒的半径R = 60cm ，两盒间隙d = 1.0cm ，盒间电压U = 2.0×10⁴V ，今将α粒子从近于间隙中心某点向D形盒内以近似于零的初速度垂直B的方向射入，求粒子在加速器内运行的总时间。

命题意图：考查综合分析及推理能力。B级要求。

错解分析:考生对α粒子运动过程缺乏分解和总体把握，不能运用等效办法求解在电场中加速的时间，陷入逐段分析求和的泥潭，导致错解。

解题方法与技巧：带电粒子在回旋加速器转第一周，经两次加速，速度为v₁ ，则根据动能定理得：2qU =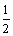m

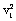
设运转n周后，速度为v ，则：

n2qU =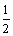mv² ①

由牛顿第二定律，qvB = m　　　　　　　 ②

由①②得粒子转动n =周。

粒子在加速器内运行的总时间t = t_B + t_E ，

在磁场中运动每周等时，则在磁场中的总时间：

t_B = nT = n==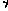

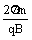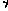
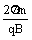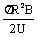
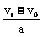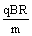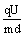而在间隙处电场中运动时间为t_E ，因每次时间不等(且次数又多，分段算将十分繁琐)，我们可将各段间隙等效“衔接”起来，展开成一准直线，则粒子在电场中运动就可视作初速度为零的匀加速直线运动，由公式：t_E =，且v₀ = 0 ，v_t =，a =得：

t_E =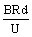

故：t = t_B + t_E =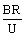(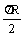+ d) = 4.5×10^－5×(0.94 + 0.01)= 4.3×10^－5s 。

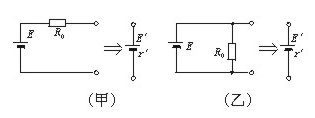
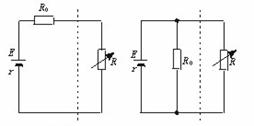［例2］(★★★★)(物理模型的变换等效)如图26-3所示的甲、乙两个电路中电源电动势E和内电阻r已知，定值电阻R已知，求电阻R调至多大时，R上获得的电功率最大，其最大值为多少？电源在什么条件下输出功率最大？

命题意图：考查综合分析能力及运用已学知识灵活解决物理问题的能力。B级要求。

错解分析：考生往往借助常规思路，据闭合电路欧姆定律及直流电路特点，写出R的功率表达式，讨论求解，繁杂易错，思维缺乏灵活性。

解题方法与技巧：本题用隔离法分析比较巧妙，设沿虚线将电路隔离成左、右两部分，左边部分可以看作一个新的电源，对(甲)图电路来说，新电源的电动势为E′= E ，而内电阻r′= r + R₀ ，对(乙)图来说，新电源的电动势为E′=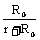E ，而r′=，如图26-4所示。虚线右边部分即为新电源的外电阻R。这种新电源又叫做等效电源。

图26-4

这样原来的甲乙电路就简化成了由等效电源(E′，r′)与电阻R连成的最简单电路。由电源的输出功率(即外电路上R获得的电功率)与外电阻R的关系知，在(甲)图中当R = r′= r + R₀时，R上获得的电功率最大，其最大功率为P_m =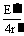=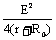。对(乙)图中当R = r′=时R上获得的功率最大，最大功率为：

P_m ===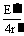

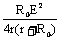
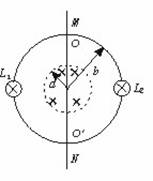
2.(★★★★★)(2001年上海)如图26-1所示，半径为a的圆形区域内有匀强磁场，磁感应强度B = 0.2T ，磁场方向垂直纸面向里，半径为b的金属圆环与磁场同心地放置，磁场与环面垂直，其中a = 0.4m ，b = 0.6m 。金属环上分别接有灯L₁ 、L₂ ，两灯的电阻均为R₀ = 2Ω 。一金属棒MN与金属环接触良好，棒与环的电阻均不计。

(1)若棒以v₀ = 5m/s的速率在环上向右匀速滑动，求棒滑过圆环直径OO′的瞬时，MN中的电动势和流过L₁的电流。

(2)撤去中间的金属棒MN，将右面的半圆环OL₂O′以OO′为轴向上翻转90°，若此时磁场随时间均匀变化，其变化率为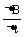=(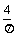)T/s ，求L₁的功率。

1.(★★★★)(2000年全国春考京、皖卷)AB两地间铺有通讯电缆，长为L，它是由两条并在一起彼此绝缘的均匀导线组成的，通常称为双线电缆。在一次事故中经检查断定是电缆上某处的绝缘保护层损坏，导致两导线之间漏电，相当于该处电缆的两导线之间接了一个电阻。检查人员经过下面的测量可以确定损坏处的位置：①令B端的双线断开，在A处测出双线两端间的电阻R_A ；②令A端的双线断开，在B处测出双线两端的电阻R_B ；③在A端的双线间加一已知电压U_A ，在B端用内阻很大的电压表测出两线间的电压U_B 。试由以上测量结果确定损坏处的位置。

图26-1

25．(本题满分14分，第(1)小题满分6分，第(2)小题满分5分，第(3)小题满分3分)

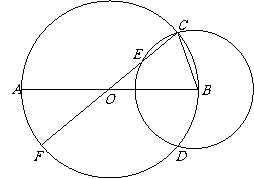已知：⊙O的直径AB=8，⊙B与⊙O相交于点C、D，⊙O的直径CF与⊙B相交于点E，设⊙B的半径为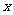，OE的长为，

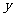(1)　 如图7，当点E在线段OC上时，求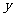关于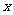的函数解析式，并写出定义域；

(2)　 当点E在直径CF上时，如果OE的长为3，求公共弦CD的长；

(3)　

24．(本题满分12分，第(1)小题满分7分，第(2)小题满分5分)　

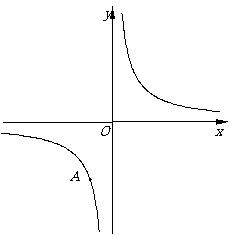已知：如图6，点A(–2，–6)在反比例函数的图像上，如果点B也在此反比例函数图像上，直线AB与 y轴相交于点C，且BC=2AC ．

(1)　　 求点B的坐标；

(2)　　 如果二次函数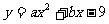的图像经过A、B两点，求此二次函数的解析式.

23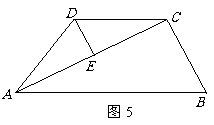．(本题满分12分)

已知：如图5，在梯形ABCD中，AB∥CD，AC⊥BC，AC平分∠DAB，点E为AC的中点．

求证：DE=．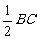

22．(本题满分10分，每小题满分各2分)　

　　 某区为了了解九年级学生身体素质情况，从中随机抽取了部分学生进行测试，测试成绩的最高分为30分，最低分为23分，按成绩由低到高分成五组(每组数据可含最大值，不含最小值)，绘制的频率分布直方图中缺少了28.5~30分的一组(如图4)．已知27~28.5分一组的频率为0.31，且这组学生人数比25.5~27分的学生多了28人．根据图示及上述相关信息解答下列问题：

(1)　　 从左至右前三组的频率依次为：___________________；

(2)　　 在图4中补画28.5~30分一组的小矩形；

(3)　　

(4)　　 测试成绩的中位数落在___________组；

(5)　　 如果全区共有3600名九年级学生，估计成绩大于27分的学生约有­__________人．

21．(本题满分10分，第(1)小题满分6分，第(2)小题满分4分)

如图3，在Rt△ABC中，∠C=90º，AB=10，cosB=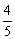，点D在边BC上，tan∠CAD=．

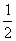(1)求BD长；

(2)设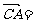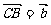，，用、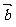的线性组合表示．