
2、(2004年连云港第二次调研题)某人在乎直公路上骑自行车,见到前方较远处红色交通信号灯亮起,他便停止蹬车,此后的一段时间内,自行车前轮和后轮受到地面的摩擦力分别为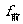 和
和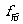 ,则… ( C
)
,则… ( C
)
A.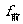 向后,
向后,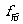 后向前 B.
后向前 B.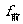 向前,
向前,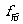 向后
向后
 C.
C.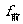 向后,
向后,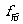 向后 D.
向后 D.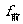 向前,
向前,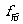 向前
向前
中学物理只谈静摩擦和滑动摩擦两种(滚动摩擦不讲).其中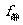 没有具体的计算公式,是随外力变化的范围值o≤
没有具体的计算公式,是随外力变化的范围值o≤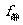 ≤
≤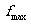 ,一般根据(1)平衡条件求;(2)根据物体运动状态,由牛顿运动定律求.而
,一般根据(1)平衡条件求;(2)根据物体运动状态,由牛顿运动定律求.而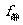 不但可根据上述的 (1)、(2)方法求,还可以用公式
不但可根据上述的 (1)、(2)方法求,还可以用公式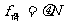 计算
计算
 例3 如图3所示,质量为
例3 如图3所示,质量为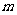 、带电量为+q的小物体,放在磁感应强度为B的匀强磁场中,粗糙挡板ab的宽度略大于小物体厚度.现给带电体一个水平冲量
、带电量为+q的小物体,放在磁感应强度为B的匀强磁场中,粗糙挡板ab的宽度略大于小物体厚度.现给带电体一个水平冲量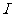 ,试分析带电体所受摩擦力的情况.
,试分析带电体所受摩擦力的情况.
解析:带电体获得水平初速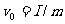 它在.它在
它在.它在
磁场中受洛仑兹力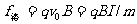 和重力
和重力 ,若
,若
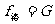 ,则带电体作匀速直线运动,不受摩擦力作用.
,则带电体作匀速直线运动,不受摩擦力作用.
若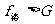 ,则带电体贴着a板前进,滑动摩擦力
,则带电体贴着a板前进,滑动摩擦力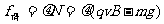 ,速度越来越小,
,速度越来越小,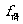 变小,当
变小,当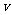 减小到
减小到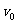 ,又有
,又有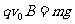 ,它又不受摩擦力作用而匀速前进.
,它又不受摩擦力作用而匀速前进.
若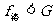 ,则带电体贴着b板前逆。滑动摩擦力;
,则带电体贴着b板前逆。滑动摩擦力;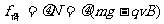 ,它减速运动动直至静止,而
,它减速运动动直至静止,而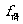 却是变大的.
却是变大的.
这充分说明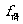 也是具有被动性,所以摩擦力是被动力.了解摩擦力的上述特点在解题时就能因题致宜,灵活地思考,少走弯路,避免出错.
也是具有被动性,所以摩擦力是被动力.了解摩擦力的上述特点在解题时就能因题致宜,灵活地思考,少走弯路,避免出错.
对于滑动摩擦力的大小,还必须了解其与物体运动状态无关,与接触面积大小无关的特点.
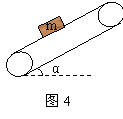
例4 如图4所示,一质量为m的货物放在倾角为α的传送带上随传送带一起向上或向下做加速运动.设加速度大小为α,试求两种情况下货物所受的摩擦力.
解析:物体m向上加速运动时,由于沿斜面向下有重力的分力,所以要使物体随传送带向上加速运动,传送带对物体的摩擦力必定沿传送带向上.物体沿斜面向下加速运动时,摩擦力的方向要视加速度的大小而定,当加速度为某一合适值时,重力沿斜面方向的分力恰好提供了所需的合外力,则摩擦力为零;当加速度大于此值时,摩擦力应沿斜面向下;当加速度小于此值时,摩擦力应沿斜面向上.
向上加速运动时,由牛顿第二定律,得:所以F-mgsina=ma,方向沿斜面向上
向下加速运动时,由牛顿第二定律,得: mgsina-F=ma(设F沿斜面向上)
所以F=mgsina-ma
当a<gsina时,F>0.与所设方向相同--沿斜面向上.
当a=gsina时,F=0.即货物与传送带间无摩擦力作用.
当a>gsina时,F<0.与所设方向相反--沿斜面向下.
小结:当物体加速运动而摩擦力方向不明确时,可先假设摩擦力向某一方向,然后应用牛顿第二定律导出表达式,再结合具体情况进行讨论
例5 如图5所示,质量M=10Kg的木楔ABC静止于水平地面上,动摩擦因数μ=0.02,在木楔的倾角θ为300的斜面上有一质量m=1.0 kg的物块由静止开始沿斜面下滑.当滑行路程S=1.4m时,其速度s=1.4m/s,在此过程中木楔没有动.求地面对木楔的摩擦力的大小和方向(g取10 m/s’)
解析:地面对木楔的摩擦力为静摩擦力,但不一定为最大静摩擦力,所以不能由Fμ=μFΝ,来计算求得,只能根据物体匀运动情况和受力情况来确定.
物块沿斜面匀加速下滑,由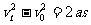 可求得物块下滑的加速度
可求得物块下滑的加速度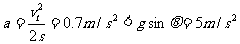
可知物块受到摩塔力的作用.
此条件下,物块与木楔受力情况分别如图6.7所示.
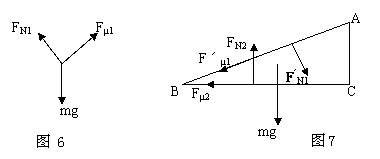
物块沿斜面以加速度Q下滑,对它沿斜面方向和垂直于斜面方向由牛顿第二定律有mgsinθ一Fμ1=ma mgcosθ-FN1=0 .
木楔静止,对它沿水平方向和竖直方向由牛顿第二定律,
并注意Fμ1ˊ与Fμ1,F ́N1与FN1,等值反向,有Fμ2+ Fμ1cosθ-FN1sinθ=0
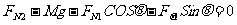
由上面各式解得地面对木楔的摩擦力
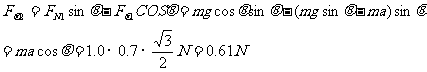
此力方向与所设方向相同,由C指向B。
另外由以上几式联立还可以求出地面对木楔的支持力
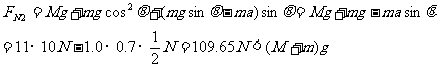
显然,这是由于物块和木楔系统有向下的加速度而产生了失重现象。
对此题也可以系统为研究对象。在水平方向,木楔静止,加速度为零,物块加速度水平分量为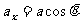 。对系统在水平方向由牛顿第二定律,有
。对系统在水平方向由牛顿第二定律,有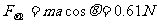
答案:0.61 N 方向由C一B
小结:(1)静摩擦力的大小是个变量,它的大小常需要根据物体的运动状态及摩擦力与物体所受其他力的关系来确定.
(2)由此题可看出,研究对象的选取对解题步骤的简繁程度有很大的影响。
 练习
练习
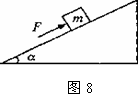
1、如图8所示,位于斜面上的物块m在沿斜面向上的力F作用下,处于静止状态,则斜面作用于物块的静摩擦力 ①方向可能沿斜面向上 ②方向可能沿斜面向下 ③大小可能为零 ④大小可能等于F以上判断正确的是………………………………( D )
A.只有①② B.只有③④ C.只有①②③ D.①②③④都正确
摩擦力具有两个显著特点:(1)接触性; (2)被动性.所谓接触性,即指物体受摩擦力作用物体间必直接接触(反之不一定成立)。这种特点已经包括在摩擦力产生的条件里,这里不赘述。对于摩擦力的被动性,现仔细阐述。所谓被动性是指摩擦力随外界约束因素变化而变化.熟知的是静摩擦力随外力的变化而变化。
 例2 (1992年全国考题)如图2所示,一木块放在水平桌面上,在水平方向共受到三个力,即
例2 (1992年全国考题)如图2所示,一木块放在水平桌面上,在水平方向共受到三个力,即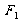 、
、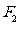 和摩擦力作用,木块图2处于静止状态,其中
和摩擦力作用,木块图2处于静止状态,其中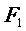 =10N、
=10N、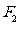 =2N,若撤去力
=2N,若撤去力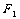 ,则木块在水平方向受到的合力为
,则木块在水平方向受到的合力为
(A)10N,方向向左 (B)6N,方向向右
(C)2N,方向向左 (D)零
解析;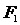 没有撤去时,物体所受合外力为零,此时静摩擦力大小为8N,方向向左.撤去
没有撤去时,物体所受合外力为零,此时静摩擦力大小为8N,方向向左.撤去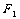 以后,物体在
以后,物体在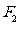 作用下不可能沿水平方向发生运动状态的改变,物体仍保拧静止.此时地面对物体的静摩擦力大小为2N,方向向右.从上述分析可见静摩擦力是被动力.答案应为(D).对于滑动摩擦力同样具有被动性.
作用下不可能沿水平方向发生运动状态的改变,物体仍保拧静止.此时地面对物体的静摩擦力大小为2N,方向向右.从上述分析可见静摩擦力是被动力.答案应为(D).对于滑动摩擦力同样具有被动性.
(1) 物体间直接接触
(2) 接触面粗糙
(3) 接触面间有弹力存在
(4) 物体间有相对运动或相对运动趋势
这四个条件紧密相连,缺一不可.显然,两物体不接触,或虽接触但接触面是光滑的,则肯定不存在摩擦力.但满足(1)、(2)而缺少(3)、 (4)中的任意一条,也不会有摩擦力.如一块砖紧靠在竖直墙,放手后让其沿墙壁下滑,它满足条件(1)、(2)、(4),却不具备条件(3),即相互间无压力,故砖不可能受到摩擦力作用.又如,静止在粗糙水平面上的物体它满足了条件(1)、 (2)、(3),缺少条件(4),当然也不存在摩擦力.
 由于不明确摩擦力产生的条件,导致答题错误的事是经常发生的.
由于不明确摩擦力产生的条件,导致答题错误的事是经常发生的.
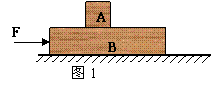
例1 (1994年全国考题)如图1所示,C是水平地面,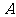 、
、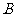 是两个长方形物块,F是作用在物块上沿水平方向的力,物体
是两个长方形物块,F是作用在物块上沿水平方向的力,物体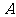 和
和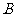 以相同的速度作匀速直綫运动,由此可知,
以相同的速度作匀速直綫运动,由此可知,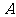 、
、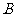 间的动摩擦因数
间的动摩擦因数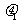 和
和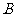 、
、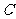 间的动摩擦因数
间的动摩擦因数 有可能是
有可能是
(A)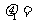 0,
0,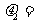 0 (B)
0 (B) 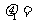 0,
0,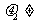 0
0
(C) 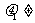 0,
0,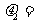 0 (D)
0 (D) 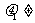 0,
0,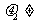 0
0
解析:本题中选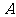 、
、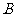 整体为研究对象,由于受推力的作用做匀速直线运动,可知地面对的摩擦力一定水平向左,故
整体为研究对象,由于受推力的作用做匀速直线运动,可知地面对的摩擦力一定水平向左,故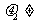 0,对A受力分析可知,水平方向不受力,
0,对A受力分析可知,水平方向不受力,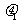 可能为0,可能不为0。正确答案为(B)、(D).
可能为0,可能不为0。正确答案为(B)、(D).
10、一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以3m/s2的加速度开始行驶,恰在这时一辆自行车以6m/s的速度匀速驶来,从后边赶过汽车。试求:
(1) 汽车从路口开动后,在追上自行车之前经过多长时间两车相距最远?此时距离是多少?
(2) 什么时候汽车追上自行车,此时汽车的速度是多少?
解析:解法一:汽车开动后速度由零逐渐增大,而自行车的速度是定值。当汽车的速度还小于自行车速度时,两者的距离将越来越大,而一旦汽车速度增加到超过自行车速度时,两车距离就将缩小。因此两者速度相等时两车相距最大,有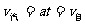 ,所以,
,所以,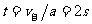
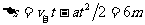
解法二:用数学求极值方法来求解
(1) 设汽车在追上自行车之前经过t时间两车相距最远,
因为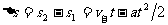
所以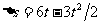 ,由二次函数求极值条件知,
,由二次函数求极值条件知,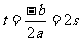 时,
时, 最大
最大
即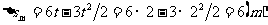
(2)汽车追上自行车时,二车位移相等,则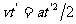
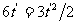 ,
, 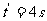
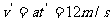
解法三:用相对运动求解更简捷
选匀速运动的自行车为参考系,则从运动开始到相距最远这段时间内,汽车相对此参考系的各个物理量为:
初速度v0 = v汽初-v自 =(0-6)m/s = -6m/s
末速度vt = v汽末-v自 =(6-6)m/s = 0
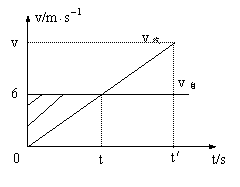 加速度 a = a汽-a自 =(3-0)m/s2 = 3m/s2
加速度 a = a汽-a自 =(3-0)m/s2 = 3m/s2
所以相距最远 s=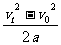 =-6m(负号表示汽车落后)
=-6m(负号表示汽车落后)
解法四:用图象求解
(1)自行车和汽车的v-t图如图,由于图线与横坐标轴所包围的面积表示位移的大小,所以由图上可以看出:在相遇之前,在t时刻两车速度相等时,自行车的位移(矩形面积)与汽车的位移(三角形面积)之差(即斜线部分)达最大,所以
t=v自/a= s=2s
s=2s
△s= vt-at2/2 =(6×2-3×22/2)m= 6m
(2)由图可看出:在t时刻以后,由v自或与v汽线组成的三角形面积与标有斜线的三角形面积相等时,两车的位移相等(即相遇)。所以由图得相遇时,t’= 2t = 4s,v’= 2v自=12m/s
答案 (1)2s 6m (2)12m/s
8、摩托车在平直公路上从静止开始起动,a1=1.6m/s2,稍后匀速运动,然后减速,a2=6.4m/s2,直到停止,共历时130s,行程1600m。试求:
(1) 摩托车行驶的最大速度vm;
(2) 若摩托车从静止起动,a1、a2不变,直到停止,行程不变,所需最短时间为多少?
分析:(1)整个运动过程分三个阶段:匀加速运动;匀速运动;匀减速运动。可借助v-t图象表示。
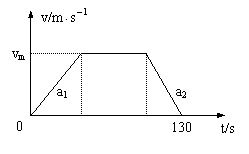 (2)首先要回答摩托车以什么样的方式运动可使得时间最短。借助v-t图象可以证明:当摩托车以a1匀加速运动,当速度达到v/m时,紧接着以a2匀减速运动直到停止时,行程不变,而时间最短
(2)首先要回答摩托车以什么样的方式运动可使得时间最短。借助v-t图象可以证明:当摩托车以a1匀加速运动,当速度达到v/m时,紧接着以a2匀减速运动直到停止时,行程不变,而时间最短
解:(1)如图所示,利用推论vt2-v02=2as有: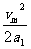 +(130-
+(130-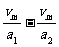 )vm+
)vm+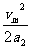
 =1600.其中a1=1.6m/s2,a2=6.4m/s2.解得:vm=12.8m/s(另一解舍去).
=1600.其中a1=1.6m/s2,a2=6.4m/s2.解得:vm=12.8m/s(另一解舍去).
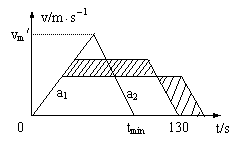 (2)路程不变,则图象中面积不变,当v越大则t越小,如图所示.设最短时间为tmin,则tmin=
(2)路程不变,则图象中面积不变,当v越大则t越小,如图所示.设最短时间为tmin,则tmin= ①
①
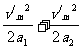 =1600 ②
=1600 ②
其中a1=1.6m/s2,a2=6.4m/s2.由②式解得vm=64m/s,故tmin=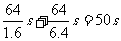 .既最短时间为50s.
.既最短时间为50s.
答案:(1)12.8m/s (2)50s
9一平直的传送以速率v=2m/s匀速行驶,传送带把A处的工件送到B处,A、B两处相距L=10m,从A处把工件无初速度地放到传送带上,经时间t=6s能传送到B处,欲使工件用最短时间从A处传送到B处,求传送带的运行速度至少应多大?
解析:物体在传送带上先作匀加速运动,当速度达到v=2m/s后与传送带保持相对静止,作匀速运动.设加速运动时间为t,加速度为a,则匀速运动的时间为(6-t)s,则:
v=at ①
s1= at2 ②
at2 ②
s2=v(6-t) ③
s1+s2=10 ④
联列以上四式,解得t=2s,a=1m/s2
物体运动到B处时速度即为皮带的最小速度
由v2=2as 得v=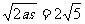 m/s
m/s
传送带给物体的滑动摩擦力提供加速度,即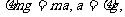 此加速度为物体运动的最大加速度.要使物体传送时间最短,应让物体始终作匀加速运动
此加速度为物体运动的最大加速度.要使物体传送时间最短,应让物体始终作匀加速运动
7、天文观测表明,几乎所有远处的恒星(或星系)都在以各自的速度背离我们而运动,离我们越远的星体,背离我们运动的速度(称为退行速度)越大;也就是说,宇宙在膨胀,不同星体的退行速度v和它们离我们的距离r成正比,即v=Hr。式中H为一常量,称为哈勃常数,已由天文观察测定,为解释上述现象,有人提供一种理论,认为宇宙是从一个大爆炸的火球开始形成的,假设大爆炸后各星体即以不同的速度向外匀速运动,并设想我们就位于其中心,则速度越大的星体现在离我们越远,这一结果与上述天文观测一致。
由上述理论和天文观测结果,可估算宇宙年龄T,其计算式如何?根据近期观测,哈勃常数H=3×10-2m/(s 光年),其中光年是光在一年中行进的距离,由此估算宇宙的年龄约为多少年?
解析:由题意可知,可以认为宇宙中的所有星系均从同一点同时向外做匀速直线运动,由于各自的速度不同,所以星系间的距离都在增大,以地球为参考系,所有星系以不同的速度均在匀速远离。则由s=vt可得r=vT,所以,宇宙年龄:T=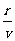 =
=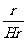 =
=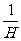
若哈勃常数H=3×10-2m/(s 光年)
则T=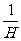 =1010年
=1010年
思考:1 宇宙爆炸过程动量守恒吗?如果爆炸点位于宇宙的“中心”,地球相对于这个“中心”做什么运动?其它星系相对于地球做什么运动?
2 其它星系相对于地球的速度与相对于这个“中心”的速度相等吗?
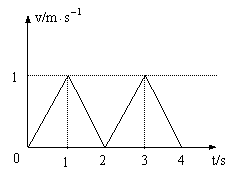
6、一物体在A、B两点的正中间由静止开始运动(设不会超越A、B),其加速度随时间变化如图所示。设向A的加速度为为正方向,若从出发开始计时,则物体的运动情况是( )
A 先向A ,后向B,再向A,又向B,4秒末静止在原处
B 先向A ,后向B,再向A,又向B,4秒末静止在偏向A的某点
 C 先向A ,后向B,再向A,又向B,4秒末静止在偏向B的某点
C 先向A ,后向B,再向A,又向B,4秒末静止在偏向B的某点
D 一直向A运动,4秒末静止在偏向A的某点
解析:根据a-t图象作出其v-t图象,如右图所示,由该图可以看出物体的速度时大时小,但方向始终不变,一直向A运动,又因v-t图象与t轴所围“面积”数值上等于物体在t时间内的位移大小,所以4秒末物体距A点为2米
答案:D
5、在轻绳的两端各栓一个小球,一人用手拿者上端的小球站在3层楼阳台上,放手后让小球自由下落,两小球相继落地的时间差为T,如果站在4层楼的阳台上,同样放手让小球自由下落,则两小球相继落地时间差将 ( )
A 不变 B 变大 C 变小 D 无法判断
解析:两小球都是自由落体运动,可在一v-t图象中作出速度随时间的关系曲线,如图所示,设人在3楼阳台上释放小球后,两球落地时间差为△t1,图中阴影部分面积为△h,若人在4楼阳台上释放小球后,两球落地时间差△t2,要保证阴影部分面积也是△h;从图中可以看出一定有△t2〈△t1
答案:C
4、 汽车甲沿着平直的公路以速度v0做匀速直线运动,当它路过某处的同时,该处有一辆汽车乙开始做初速度为零的匀加速运动去追赶甲车,根据上述的已知条件( )
汽车甲沿着平直的公路以速度v0做匀速直线运动,当它路过某处的同时,该处有一辆汽车乙开始做初速度为零的匀加速运动去追赶甲车,根据上述的已知条件( )
A. 可求出乙车追上甲车时乙车的速度
B. 可求出乙车追上甲车时乙车所走的路程
C. 可求出乙车从开始起动到追上甲车时所用的时间
D. 不能求出上述三者中任何一个
分析:题中涉及到2个相关物体运动问题,分析出2个物体各作什么运动,并尽力找到两者相关的物理条件是解决这类问题的关键,通常可以从位移关系、速度关系或者时间关系等方面去分析。
解析:根据题意,从汽车乙开始追赶汽车甲直到追上,两者运动距离相等,即s甲=
=s乙=s,经历时间t甲=t乙=t.
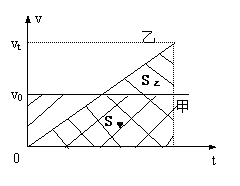 那么,根据匀速直线运动公式对甲应有:
那么,根据匀速直线运动公式对甲应有: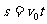
根据匀加速直线运动公式对乙有: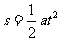 ,及
,及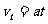
由前2式相除可得at=2v0,代入后式得vt=2v0,这就说明根据已知条件可求出乙车追上甲车时乙车的速度应为2v0。因a不知,无法求出路程和时间,如果我们采取作v-t图线的方法,则上述结论就比较容易通过图线看出。图中当乙车追上甲车时,路程应相等,即从图中图线上看面积s甲和s乙,显然三角形高vt等于长方形高v0的2倍,由于加速度a未知,乙图斜率不定,a越小,t越大,s也越大,也就是追赶时间和路程就越大。
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com