
1.质量为m的人随平板车以速度V在平直跑道上匀速前进,不考虑摩擦阻力,当此人相对于车竖直跳起至落回原起跳位置的过程中,平板车的速度 ( )
A.保持不变 B.变大 C.变小
D.先变大后变小 E.先变小后变大
5.如图所示,人与冰车质量为M,球质量为m,开始均静止于光滑冰面上,现人将球以对地速度V水平向右推出,球与挡板P碰撞后等速率弹回,人接住球后又将球以同样的速度V向右推出……如此反复,已知M = 16 m,试问人推球几次后将接不到球?
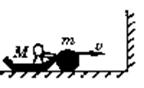
分析:(该题是多过程动量守恒问题,可以采用数学归纳的方法研究;当然也可整个过程采用动量定理研究)
解析: 取水平向左为正方向,冰车、人、球为系统.由动量守恒定律,
对第一次推球过程有: 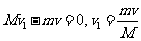
对第二次整个接、推球过程有: 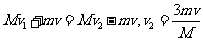
对第三次整个接、推球过程有: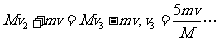
对第n次整个接、推球过程同理分析得: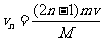
设推球n次后恰接不到球,则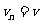 ,故有
,故有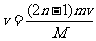 代人已知条件
代人已知条件
解得:n = 8.5, 即人推球9次后将接不到球.
三:动量守恒定律适应练习
丹阳六中 马跃中
4.如图所示,一块足够长的木板,放在光滑水平面上,在木板上自左向右并非放有序号是1,2,3,…,n的物体,所有物块的质量均为m,与木板间的动摩擦因数都相同,开始时,木板静止不动,第1,2,3,…n号物块的初速度分别是v ,2 v
,2 v ,3 v
,3 v ,…nv
,…nv ,方向都向右,木板的质量与所有物块的总质量相等 ,最终所有物块与木板以共同速度匀速运动。设物块之间均无相互碰撞,木板足够长。试求:
,方向都向右,木板的质量与所有物块的总质量相等 ,最终所有物块与木板以共同速度匀速运动。设物块之间均无相互碰撞,木板足够长。试求:
(1)所有物块与木板一起匀速运动的速度v ;
;
(2)第1号物块与木板刚好相对静止时的速度v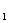 ;
;
(3)通过分析与计算说明第k号(k<n=物块的最小速度v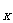

分析:(多个物体组成的系统,应恰当选择小系统利用动量守恒定律求解)
在木板上各个物块相对木板运动,都给木板一个向右的磨擦力,因各个物块质量相同,滑动磨擦力都一样,木板在磨擦力的作用下向右加速。由于每个物块的初始速度不同,因而相对木板静止的物块顺序依次是1,2,…,n号,当第一号物块由v 到相对木板静止时,其动量变化设为△p
到相对木板静止时,其动量变化设为△p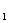 ,则其他各个所有物块在这段时间内的动量变化也都为△p
,则其他各个所有物块在这段时间内的动量变化也都为△p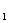 (f相同,T相同),因木板与所有物块总动量守恒,故可用动量守恒关系求出第1号物块相对木板静止时的速度。
(f相同,T相同),因木板与所有物块总动量守恒,故可用动量守恒关系求出第1号物块相对木板静止时的速度。
解析:(1)设所有物块都相对木板静止时的速度为 v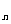 ,因木板与所有物块系统水平方向不受外力,动量守恒,应有:
,因木板与所有物块系统水平方向不受外力,动量守恒,应有:
m v +m·2 v
+m·2 v +m·3 v
+m·3 v +…+m·n v
+…+m·n v =(M + nm)v
=(M + nm)v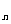 1
1
M = nm, 2
解得: v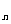 =
=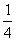 (n+1)v
(n+1)v ,
,
(2)设第1号物块相对木板静止时的速度为v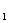 ,取木板与物块1为系统一部分,第2 号物块到第n号物块为系统另一部分,则
,取木板与物块1为系统一部分,第2 号物块到第n号物块为系统另一部分,则
木板和物块1 △p =(M + m)v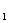 -m v
-m v ,
,
2至n号物块 △p =(n-1)m·(v
=(n-1)m·(v - v
- v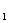 )
)
由动量守恒定律: △p=△p ,
,
解得
v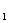 =
=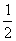 v
v ,
3
,
3
(3)设第k号物块相对木板静止时的速度由v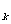 ,则第k号物块速度由k
v
,则第k号物块速度由k
v 减为v
减为v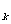 的过程中,序数在第k号物块后面的所有物块动量都减小m(k v
的过程中,序数在第k号物块后面的所有物块动量都减小m(k v - v
- v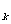 ),取木板与序号为1至K号以前的各物块为一部分,则
),取木板与序号为1至K号以前的各物块为一部分,则
△p=(M+km)v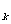 -(m v
-(m v +m·2 v
+m·2 v +…+mk v
+…+mk v )=(n+k)m v
)=(n+k)m v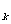 -
-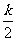 (k+1)m v
(k+1)m v
序号在第k以后的所有物块动量减少的总量为
△p =(n-k)m(k v
=(n-k)m(k v - v
- v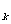 )
)
由动量守恒得 △p=△p , 即
, 即
(n+k)m v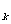 -
-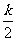 (k+1)m v
(k+1)m v = (n-k)m(k v
= (n-k)m(k v - v
- v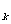 ),
),
解得 v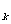 =
=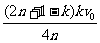
3.质量为50㎏的人站在质量为150㎏(不包括人的质量)的船头上,船和人以0.20m/s的速度向左在水面上匀速运动,若人用t =10s的时间匀加速从船头走到船尾,船长L=5m,则船在这段时间内的位移是多少?(船所受水的阻力不计)

分析:(该题利用动量守恒重点考查了人、船模型中速度关系、位移关系)
解析:设人走到船尾时,人的速度为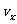 ,船的速度为
,船的速度为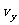
对系统分析:动量守恒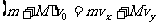
对船分析:(匀加速运动) S =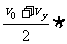
对人分析:(匀加速运动) 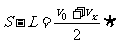
得:S = 3.25 m.
2.A、B两滑块在一水平长直气垫导轨上相碰.用频闪照相机在t0=0,t1=Δt,t2=2Δt,t3=3Δt各时刻闪光四次,摄得如图所示照片,其中B像有重叠,mB=(3/2)mA,由此可判断 ( )
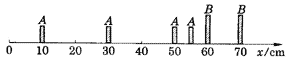 A.碰前B静止,碰撞发生在60cm处,t=2.5Δt时刻
B.碰后B静止,碰撞发生在60cm处,t=0.5Δt时刻
C.碰前B静止,碰撞发生在60cm处,t=0.5Δt时刻
D.碰后B静止,碰撞发生在60cm处,t=2.5Δt时刻
A.碰前B静止,碰撞发生在60cm处,t=2.5Δt时刻
B.碰后B静止,碰撞发生在60cm处,t=0.5Δt时刻
C.碰前B静止,碰撞发生在60cm处,t=0.5Δt时刻
D.碰后B静止,碰撞发生在60cm处,t=2.5Δt时刻
解析:该题重点考查根据照片建立碰撞的物理图景,答案为 B
1.放在光滑水平面上的A、B两小车中间夹了一压缩轻质弹簧,用两手控制小车处于静止状态,下列说法正确的是 ( )
A.两手同时放开,两车的总动量等于零
B.先放开右手,后放开左手,两车的总动量向右
C.先放开右手,后放开左手,两车的总动量向左
D.先放开右手,后放开左手,两车的总动量为零
解析:该题考查动量守恒的条件,答案为 AB
4.动量恒定律的五个特性
①系统性:应用动量守恒定律时,应明确研究对象是一个至少由两个相互作用的物体组成的系统,同时应确保整个系统的初、末状态的质量相等
②矢量性:系统在相互作用前后,各物体动量的矢量和保持不变.当各速度在同一直线上时,应选定正方向,将矢量运算简化为代数运算
③同时性: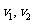 应是作用前同一时刻的速度,
应是作用前同一时刻的速度,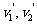 应是作用后同-时刻的速度
应是作用后同-时刻的速度
④相对性:列动量守恒的方程时,所有动量都必须相对同一惯性参考系,通常选取地球作参考系
⑤普适性:它不但适用于宏观低速运动的物体,而且还适用于微观高速运动的粒子.它与牛顿运动定律相比,适用范围要广泛得多,又因动量守恒定律不考虑物体间的作用细节,在解决问题上比牛顿运动定律更简捷
二:典题分析
3.动量守恒定律的适用条件 :
①系统不受外力或受到的外力之和为零(∑F合=0);
②系统所受的外力远小于内力(F外 F内),则系统动量近似守恒;
F内),则系统动量近似守恒;
③系统某一方向不受外力作用或所受外力之和为零,则系统在该方向上动量守恒(分方向动量守恒)
2.一般数学表达式: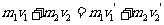
1.定律内容:相互作用的几个物体组成的系统,如果不受外力作用,或者它们受到的外力之和为零,则系统的总动量保持不变。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com