
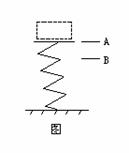
3.一物体从某一高度自由落下,落在直立于地面的轻弹簧上,如图所示.在A点时,物体开始接触弹簧;到B点时,物体速度为零,然后被弹回.下列说法中正确的是 [bcd ]
A.物体从A下降到B的过程中,动能不断变小
B.物体从B上升到A的过程中,动能先增大后减小
C.物体由A下降到B的过程中,弹簧的弹性势能不断增大
 D.物体由B上升到A的过程中,弹簧所减少的弹性势能等于物体所增加的动能与增加的重力势能之和
D.物体由B上升到A的过程中,弹簧所减少的弹性势能等于物体所增加的动能与增加的重力势能之和
2.质量为m的物体,在距地面h高处以g /3的加速度由静止竖直下落到地面,
下列说法中正确的是: ( )
A. 物体的重力势能减少 1/3 mgh
B. 物体的机械能减少 2/3 mgh
C. 物体的动能增加 1/3 mgh
D. 重力做功 mgh
1.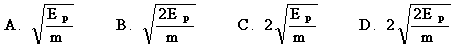 在光滑水平面上有两个相同的弹性小球A、B,质量都为m. 现B球静止,A球向B球运动,发生正碰。已知碰撞过程中总机械能守恒,两球压缩最紧时的弹性势能为Ep,则碰前A球的速度等于 (
)
在光滑水平面上有两个相同的弹性小球A、B,质量都为m. 现B球静止,A球向B球运动,发生正碰。已知碰撞过程中总机械能守恒,两球压缩最紧时的弹性势能为Ep,则碰前A球的速度等于 (
)
3.
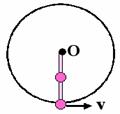 例1、如图示,长为l 的轻质硬棒的底端和中点各固定一个质量为m的小球,为使轻质硬棒能绕转轴O转到最高点,则底端小球在如图示位置应具有的最小速度v= 。
例1、如图示,长为l 的轻质硬棒的底端和中点各固定一个质量为m的小球,为使轻质硬棒能绕转轴O转到最高点,则底端小球在如图示位置应具有的最小速度v= 。
解:系统的机械能守恒,ΔEP +ΔEK=0
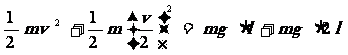 因为小球转到最高点的最小速度可以为0 ,所以,
因为小球转到最高点的最小速度可以为0 ,所以,
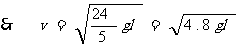
例 2. 如图所示,一固定的楔形木块,其斜面的倾角θ=30°,另一边与地面垂直,顶上有一定滑轮。一柔软的细线跨过定滑轮,两端分别与物块A和B连结,A的质量为4m,B的质量为m,开始时将B按在地面上不动,然后放开手,让A沿斜面下滑而B上升。物块A与斜面间无摩擦。设当A沿斜面下滑S 距离后,细线突然断了。求物块B上升离地的最大高度H.
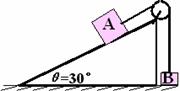 解:对系统由机械能守恒定律
解:对系统由机械能守恒定律
4mgSsinθ – mgS = 1/2× 5 mv2
∴ v2=2gS/5
细线断后,B做竖直上抛运动,由机械能守恒定律
mgH= mgS+1/2× mv2
∴ H = 1.2 S
例 3. 如图所示,半径为R、圆心为O的大圆环固定在竖直平面内,两个轻质小圆环套在大圆环上.一根轻质长绳穿过两个小圆环,它的两端都系上质量为m的重物,忽略小圆环的大小。
(1)将两个小圆环固定在大圆环竖直对称轴的两侧θ=30°的位置上(如图).在
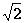 两个小圆环间绳子的中点C处,挂上一个质量M= m的重物,使两个小圆
两个小圆环间绳子的中点C处,挂上一个质量M= m的重物,使两个小圆
 环间的绳子水平,然后无初速释放重物M.设绳子
环间的绳子水平,然后无初速释放重物M.设绳子
与大、小圆环间的摩擦均可忽略,求重物M下降的最大距离.
(2)若不挂重物M.小圆环可以在大圆环上自由移动,且绳子与大、小圆环间及大、小圆环之间的摩擦均可以忽略,问两个小圆环分别在哪些位置时,系统可处于平衡状态?
解:(1)重物向下先做加速运动,后做减速运动,当重物速度
为零时,下降的距离最大.设下降的最大距离为h ,
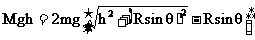
由机械能守恒定律得
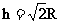 解得
解得
(另解h=0舍去)
(2)系统处于平衡状态时,两小环的可能位置为
a. 两小环同时位于大圆环的底端.
b.两小环同时位于大圆环的顶端.
c.两小环一个位于大圆环的顶端,另一个位于大圆环的底端.
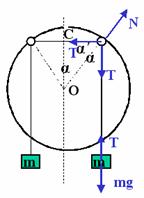 d.除上述三种情况外,根据对称性可知,系统如能平衡,则两小圆环的位置一定关于大圆环竖直对称轴对称.设平衡时,两小圆环在大圆环竖直对称轴两侧α角的位置上(如图所示).
d.除上述三种情况外,根据对称性可知,系统如能平衡,则两小圆环的位置一定关于大圆环竖直对称轴对称.设平衡时,两小圆环在大圆环竖直对称轴两侧α角的位置上(如图所示).
对于重物,受绳子拉力与重力作用, 有T=mg
对于小圆环,受到三个力的作用,水平绳的拉力T、 竖直绳子的拉力T、大圆环的支持力N.
两绳子的拉力沿大圆环切向的分力大小相等,方向相反

得α=α′, 而α+α′=90°,所以α=45 °
 例 4. 如图质量为m1的物体A经一轻质弹簧与下方地面上的质量为m2的物体B相连,弹簧的劲度系数为k,A、B都处于静止状态。一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩。开始时各段绳都牌伸直状态,A上方的一段沿竖直方向。现在挂钩上挂一质量为m3的物体C上升。若将C换成另一个质量为(m1+m3)物体D,仍从上述初始位置由静止状态释放,则这次B则离地时D的速度的大小是多少?已知重力加速度为g。
例 4. 如图质量为m1的物体A经一轻质弹簧与下方地面上的质量为m2的物体B相连,弹簧的劲度系数为k,A、B都处于静止状态。一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩。开始时各段绳都牌伸直状态,A上方的一段沿竖直方向。现在挂钩上挂一质量为m3的物体C上升。若将C换成另一个质量为(m1+m3)物体D,仍从上述初始位置由静止状态释放,则这次B则离地时D的速度的大小是多少?已知重力加速度为g。
解:开始时,B静止平衡,设弹簧的压缩量为x1,

挂C后,当B刚要离地时,设弹簧伸长量为x2,有

此时,A和C速度均为零。从挂C到此时,根据机械能守恒定律弹簧弹性势能的改变量为

将C换成D后,有
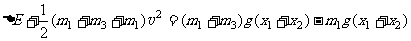
联立以上各式可以解得

针对训练
2. 对机械能守恒定律的理解:
(1)系统在初状态的总机械能等于末状态的总机械能.
即 E1 = E2 或 1/2mv12 + mgh1= 1/2mv22 + mgh2
(2)物体(或系统)减少的势能等于物体(或系统)增加的动能,反之亦然。
即 -ΔEP = ΔEK
(3)若系统内只有A、B两个物体,则A减少的机械能EA等于B增加的机械能ΔE B 即 -ΔEA = ΔEB
二、例题导航:
1. 在只有重力和弹簧的弹力做功的情况下,物体的动能和势能发生相互转化,但机械能的总量保持不变.
10.选木箱、人和小车组成的系统为研究对象,取向右为正方向.设第n次推出木箱后人与小车的速度为vn,第n次接住后速度为vn′,则由动量守恒定律可知:
第一次推出后有:0=Mv1-mv,则v1=mv/M
第一次接住后有:Mv1+mv=(M+m)v1′
第二次推出后有:(M+m)v1′=Mv2-mv,则v2=3mv/M
第二次接住后有:Mv2+mv=(M+m)v2′……
第n-1次接住:Mvn-1+mv=(M+m)vn-1
第n次推出:(M+m)vn-1′=Mvn-mv 即vn=(2n-1)mv/M
设最多能推N次,推出后有vn≥v vn-1≤v 即 ≥v,且
≥v,且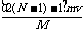 <v
<v
所以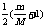 ≤ N <
≤ N <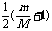 + 1 将M/m=4代入,可得: 2.5≤N<3.5
+ 1 将M/m=4代入,可得: 2.5≤N<3.5
因N取整数,故N=3
9.(1)射出第一颗子弹时,设船的速度为V1,由动量守恒定律得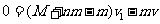 ,
,
(2)每射出一颗子弹的过程,系统的动量均守恒,而每一颗子弹进入靶中后,船的速度将为零,故每一颗子弹射出时,船后退的速度是相同的,
即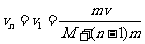
(3)每发射一颗子弹的过程实际上经历了三个阶段:第一阶段是击发到子弹射出枪瞠为止;第二个阶段是子弹在空中飞行的阶段;第三个阶段是子弹从击中靶子到静止为止.三个阶段都遵从动量守恒定律,第一、第三阶段历时很短,故这两个阶段船的移动可忽略.因此每发射一颗子弹的过程,只在第二阶段船向后移动.每发射完一颗子弹后船向移动的距离
8. (1)由动量守恒得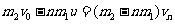 小车开始反向
小车开始反向 得
得
(2)发射相邻两 枚弹丸的时间间隔就是发射第K(K〈1〉颗弹丸后小车的周期,即 且
且
6.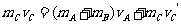 7.
7. 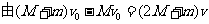

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com