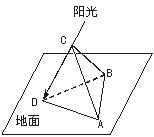
4. 如图，△ABC是简易遮阳棚，A、B是南北方向上两个定点，正东方向射出的太阳光线与地面成40°角，为了使遮阴影面ABD面积最大，遮阳棚ABC与地面所成的角为

A.75°　　　　　　　　　 B.60°　　　　　 C.50°　　　　　 D.45°

3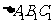．的三个内角的余弦值分别等于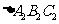的三个内角的正弦值，则(　 )

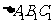A．和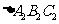都是锐角三角形

B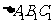．和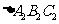都是钝角三角形

C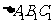．是钝角三角形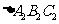，是锐角三角形

D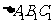．是锐角三角形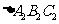，是钝角三角形

2.若A、B是锐角△ABC的两个内角，则点P(cosB－sinA，sinB－cosA)在(　 )

A.第一象限　　 B.第二象限　 C.第三象限　 D.第四象限

1. 已知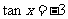，则x等于　 (　 )

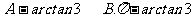
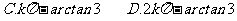
4．在应用与综合性题目中,当角不是特殊角,要“用反三角函数表示角”:

(1)

(2)arccosa表示[0，π]上余弦值等于a的角,a∈[－1,1];

(3)

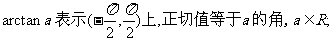
(4) 对于不是上述范围内的角,可借助诱导公式和三角函数线,找出与上述反三角的关系进而求出. 例如:sinα=0.3, α是钝角,则α=π－arcsin0.3.

3.　 正、余弦定理,斜三角形的可解类型;在应用题中要能抽象或构造出三角形;

2.　 三角函数的化简,求值,证明--恒等变形的策略与技巧.

1.　 三角函数的性质和图象变换;

3．能解决三角函数与几何、向量综合的题目,能用三角知识解决简单的实际问题。

2．掌握正、余弦定理解斜三角形的方法；