
7.若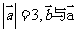 的方向相反,且
的方向相反,且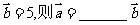
6.对平面内任意的四点A,B,C,D,则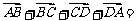 .
.
5.已知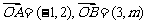 ,若
,若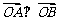 ,则
,则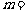 .
.
4.设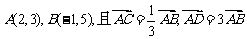 ,则C、D的坐标分别是
( )
,则C、D的坐标分别是
( )
A.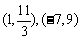 B.
B. 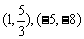 C.
C. 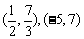 D.
D. 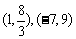
3.若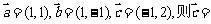 ( )
( )
A.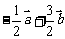 B.
B. 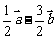 C.
C.  D.
D. 
2.已知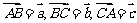 ,则
,则 是
是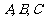 三点构成三角形的 ( )
三点构成三角形的 ( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D.既不充分也不必要条件
1.
已知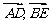 分别是
分别是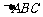 的边
的边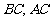 上的中线,且
上的中线,且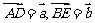 ,则
,则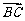 为
( )
为
( )
A. 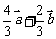 B.
B.
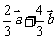 C.
C. 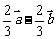 D.
D. 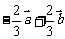
3.重要定理、公式
(1)平面向量基本定理
e1,e2是同一平面内两个不共线的向量,那么,对于这个平面内任一向量,有且仅有一对实数λ1,
λ2,使a=λ1e1+λ2e2.
(2)两个向量平行的充要条件
a∥b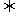 a=λb(b≠0)
a=λb(b≠0)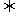 x1y2-x2y1=O.
x1y2-x2y1=O.
(3)两个向量垂直的充要条件
a⊥b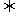 a·b=O
a·b=O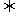 x1x2+y1y2=O.
x1x2+y1y2=O.
(4)线段的定比分点公式
设点P分有向线段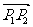 所成的比为λ,即
所成的比为λ,即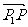 =λ
=λ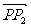 ,则
,则
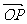 =
=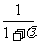
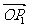 +
+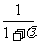
 (线段的定比分点的向量公式)
(线段的定比分点的向量公式)
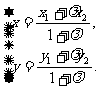 (线段定比分点的坐标公式)
(线段定比分点的坐标公式)
当λ=1时,得中点公式:
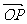 =
=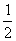 (
(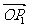 +
+ )或
)或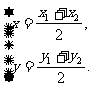
(5)平移公式
设点P(x,y)按向量a=(h,k)平移后得到点P′(x′,y′),
则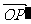 =
=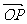 +a或
+a或
曲线y=f(x)按向量a=(h,k)平移后所得的曲线的函数解析式为:y-k=f(x-h)
2.向量的运算
|
运算类型 |
几何方法 |
坐标方法 |
运算性质 |
|
向量的 加法 |
1.平行四边形法则 2.三角形法则 |
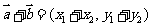 |
 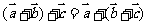 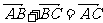 |
|
向量的 减法 |
三角形法则 |
 |
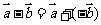 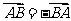 , ,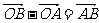 |
|
数 乘 向 量 |
1.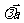 是一个向量,满足: 是一个向量,满足: 2. 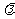 >0时, >0时,  同向; 同向;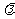 <0时, <0时, 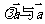 异向; 异向;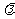 =0时, =0时,
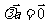 . . |
 |
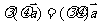 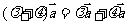  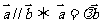 |
|
向 量 的 数 量 积 |
 是一个数 是一个数1. 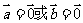 时, 时,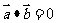 . .2.  |
  |
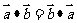  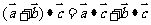 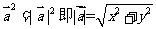  |
1.向量的概念
(1)向量的基本要素:大小和方向.(2)向量的表示:几何表示法  ;字母表示:a;
;字母表示:a;
坐标表示法 a=xi+yj=(x,y).
(3)向量的长度:即向量的大小,记作|a|.
(4)特殊的向量:零向量a=O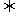 |a|=O.
|a|=O.
单位向量:aO为单位向量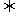 |aO|=1.
|aO|=1.
(5)相等的向量:大小相等,方向相同(x1,y1)=(x2,y2)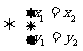
(6) 相反向量:a=-b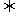 b=-a
b=-a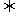 a+b=0
a+b=0
(7)平行向量(共线向量):方向相同或相反的向量,称为平行向量.记作a∥b.平行向量也称为共线向量.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com