2．(2010·淮安模拟)如图12－2－6所示为某一简谐横波在t＝0时刻的波形图，由此可知该波沿________方向传播，该时刻a、b、c三点中速度最大的是________点，加速度最大的是________点，从这一时刻开始，第一次最快回到平衡位置的是________点，若t＝0.02 s时，质点c第一次到达波谷处，则此波的波速为________m/s.

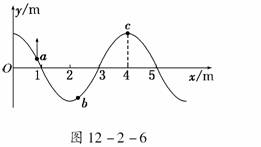
答案：x轴正　a　c　c　100

1．(2009·广东高考) 如图12－2－5所示为声波干涉演示仪

的原理图．两个U形管A和B套在一起，A管两侧各有一

小孔．声波从左侧小孔传入管内，被分成两列频率

________的波．当声波分别通过A、B传播到右侧小孔

时，若两列波传播的路程相差半个波长，则此处声波

的振幅________；若传播的路程相差一个波长，则此

处声波的振幅________．

解析：由同一波源分成的两列波频率相同，符合两列

机械波干涉的条件．当两列波的路程差等于半波长的奇数倍时，振动减弱；当路

程差等于波长的整数倍时，振动加强．

答案：相同　减小　增大

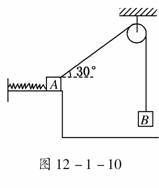
9．如图12－1－10所示， A、B两物体的质量都为m，拉A

物体的细线与水平方向的夹角为30°时处于静止状态，

不考虑摩擦力，设弹簧的劲度系数为k.若悬线突然断开

后，A在水平面上做周期为T的简谐运动，当B落地

时，A恰好将弹簧压缩到最短，求：

(1)A振动时的振幅；

(2)B落地时的速度．

解析：(1)线断前，线的拉力F＝mg，

设此时弹簧伸长为x₀，

Fcos30°＝kx₀，得x₀＝.

线断后，在弹力作用下，A做简谐运动的振幅为

A＝x₀＝.

(2)A将弹簧压缩到最短经历的时间为

t＝(+n)T(n＝0,1,2…)，

在t时间末B落地，速度v为

v＝gt＝gT(n＝0,1,2…)．

答案：(1)　(2)gT (n＝0,1,2…)

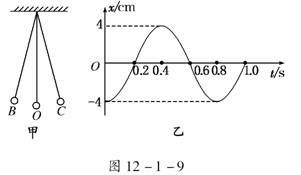
8．如图12－1－9甲所示是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置．设摆球向右方向运动为正方向．图乙所示是这个单摆的振动图象．根据图象回答：(取π²＝10)

(1)单摆振动的频率是多大？

(2)开始时刻摆球在何位置？

(3)若当地的重力加速度为10 m/s²，试求这个摆的摆长是多少？

解析：(1)由图乙可知T＝0.8 s

则f＝＝1.25 Hz

(2)由图乙知，开始时刻摆球在负向最大位移处，因向右为正方向，所以开始时摆球应在B点．(3)由T＝2π ，得：l＝≈0.16 m.

答案：(1)1.25 Hz　(2)B点　(3)0.16 m

7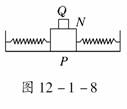．如图12－1－8所示是某同学设计的测量物体质量的装置，其中P是光滑水平面，N是质量为M的带夹子的金属盒，金属盒两端分别连接轻质弹簧；Q是固定于盒子上的遮光片，利用它和光电计时器能测量金属盒振动时的频率．已知弹簧振子做简谐运动时的周期T＝2π ，其中m是振子的质量，k 是常数．当空盒振动时，测得振动频率为f₁；把一物体夹在盒中，并使其振动时，测得频率为f₂.你认为这套装置能测量物体的质量吗？如果不能，请说明理由；若能，请求出被测物体的质量．

解析：由弹簧振子的周期公式可知，其周期是振子质量的函数，只要知道夹入物体前、后振子的周期，就可求出物体的质量．

空盒时，＝T₁＝2π

设物体质量为m，盒内装入物体后

＝T₂＝2π

联立可解m＝M.

答案：见解析

6．如图12－1－7所示的三个图线分别是用不同的传感器测出的不同物体的振动图线．从三个图线可知，这三个物体振动的共同特点是具有________；三个物体中，最简单的振动是________的振动；图中心脏跳动的图线是某人的心电图，方格纸每个小方格的宽度是0.5 cm，心电图记录仪拖动方格纸的速度是1.8 cm/s，则此人的心率是________次/分．

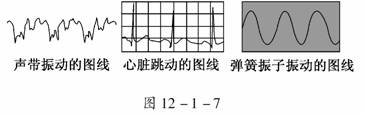
答案：周期性　弹簧振子　67.5

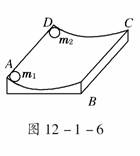
5. 如图12－1－6所示，一个光滑的圆弧形槽半径为R，放在水平地

面上，圆弧所对的圆心角小于5°.AD的长为x，今有一小球m₁以

沿AD方向的初速度v从A点开始运动，要使小球m₁可以与固定在

D点的小球m₂相碰撞，那么小球m₁的速度v应满足什么条件？

解析：把m₁的运动分成两个分运动，其一是沿AD方向的匀速运

动，其二是沿AB圆弧的运动，实际相当于摆长等于圆弧槽半径

的单摆运动．

在AD方向上：x＝vt　　　　　　　　　　　　　　　　　　　　　　　　　 ①

在AB弧上运动，等效成单摆运动：t＝nT　　　　　　　　　　　　　　　　 ②

又T＝2π　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　③

由②③两式可得：t＝2nπ(n＝1,2,3…)

代入①式得：v＝＝ (n＝1,2,3…)．

答案：v＝ (n＝1,2,3……)

4．有人利用安装在气球载人舱内的单摆来确定气球的高度．已知该单摆在海平面处的周期是T₀.当气球停在某一高度时，测得该单摆周期为T.求该气球此时离海平面的高度h.(把地球看做质量均匀分布的半径为R的球体)

解析：根据单摆周期公式得T₀＝2π ，T＝2π ，其中l是单摆长度，g₀和g

分别是两地点的重力加速度．根据万有引力定律公式可得g₀＝G，g＝G

由以上各式可解得h＝(－1)R.

答案：(－1)R

3．弹簧振子以O点为平衡位置在B、C两点之间做简谐运动，B、C相距20 cm.某时刻振子处于B点，经过0.5 s，振子首次到达C点，求：

(1)振动的周期和频率；

(2)振子在5 s内通过的路程及5 s末的位移大小；

(3)振子在B点的加速度大小跟它距O点4 cm处P点的加速度大小的比值．

解析：(1)由题意可知，振子由B→C经过半个周期，即＝0.5 s，故T＝1.0 s，

f＝＝1 Hz.

(2)振子经过1个周期通过的路程s₁＝0.4 m．振子5 s内振动了五个周期，回到B点，通过的路程：s＝5s₁＝2 m.

位移x＝10 cm＝0.1 m

(3)由F＝－kx可知：

在B点时 F_B＝－k×0.1

在P点时F_P＝－k×0.04

故＝＝5∶2.

答案：(1)1.0 s　1.0 Hz　(2)2 m　0.1 m　(3)5∶2

2．(2008·广东高考)大海中航行的轮船，受到大风大浪冲击时，为了防止倾覆，应当改变航行方向和________，使风浪冲击力的频率远离轮船摇摆的________．

解析：风浪冲击力的频率要远离轮船摇摆的频率才不会使轮船发生共振，才能防止倾覆．

答案：速度　频率