
2、(1)v02=4gR;(2)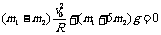 ;(3)A球受管的支持力为FA,方向竖直向上;设B球受管的弹力为FB,取竖直向上为FB的正方向,根据牛顿第二定律
;(3)A球受管的支持力为FA,方向竖直向上;设B球受管的弹力为FB,取竖直向上为FB的正方向,根据牛顿第二定律
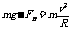
又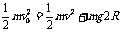 两球受圆管的合力F合=FA+BB,方向竖直向上,联立以上各式得F合=6mg,方向竖直向上 ,根据牛顿第三定律,A、B两小球对轨道作用力的合力大小为6mg,方向竖直向下。
两球受圆管的合力F合=FA+BB,方向竖直向上,联立以上各式得F合=6mg,方向竖直向上 ,根据牛顿第三定律,A、B两小球对轨道作用力的合力大小为6mg,方向竖直向下。
2.(东台市2008届第一次调研)一内壁光滑的环形细圆管,固定于竖直平面内,环的半径为R(比细管的半径大得多).在圆管中有两个直径略小于细管内径相同的小球(可视为质点).A球的质量为m1,B球的质量为m2.它们沿环形圆管顺时针运动,经过最低点时的速度都为v0.设A球运动到最低点时,B球恰好运动到最高点,重力加速度用g表示.
(1)若此时B球恰好对轨道无压力,题中相关物理量满足何种关系?
(2)若此时两球作用于圆管的合力为零,题中各物理量满足何种关系?
(3)若m1=m2=m ,试证明此时A、B两小球作用于圆管的合力大小为6mg,方向竖直向下.
答案:1、(1)0.075m;(2)v=15m;(3)提速时应采取的有效措施是增大弯道半径 r和内外轨高度差h;
1.(07届广东省惠阳市综合测试卷三)铁路转弯处的弯道半径r是根据地形决定的,弯道处要求外轨比内轨高,其内轨高度差h的设计不仅与r有关,还取决于火车在弯道上行驶的速率。下表中是铁路设计人员技术手册中弯道半径r及与之相应的轨道的高度差h。
|
弯道半径r/m |
660 |
330 |
220 |
165 |
132 |
110 |
|
内外轨高度h/m |
0.05 |
0.10 |
0.15 |
0.20 |
0.25 |
0.30 |
(1)根据表中数据,试导出h与r关系的表达式,并求出当r=400m时,h的设计值。
(2)铁路建成后,火车通过弯道时,为保证绝对安全,要求内外轨道均不向车轮施加侧面压力,又已知我国铁路内外轨的距离设计值为L=1.435m,结合表中数据,求出我国火车的转弯速率v(路轨倾角α很小时,tgα≈sinα)。
(3)随着人们的生活节奏加快,对交通运输的快捷提出了更高的要求,为了提高运输能力,国家对铁路不断进行提速改造,这就要求铁路转弯速率也需提高,请根据上述高处原理和上表分析,提速时应采取怎样的有效措施?(g取9.8m/s2)

1、
 利用极限分析法的“放大”思想分析临界状态。认清临界情景和条件,建立临界关系是解决此类问题的关键。2、圆周运动中的连接体加速度一般不同,所以,解决这类连接体的动力学问题时一般用隔离法。但也可用整体法来求解。
利用极限分析法的“放大”思想分析临界状态。认清临界情景和条件,建立临界关系是解决此类问题的关键。2、圆周运动中的连接体加速度一般不同,所以,解决这类连接体的动力学问题时一般用隔离法。但也可用整体法来求解。


1、
 要会用极限分析法判定物体可能处的状态,进而正确受力分析。2、要注意确定物体做圆周运动的圆心和半径。3、只要物体做圆周运动.在任何一个位置和状态.都满足F供=F需建立该动力关系方程是解决圆周运动问题的基本方法。
要会用极限分析法判定物体可能处的状态,进而正确受力分析。2、要注意确定物体做圆周运动的圆心和半径。3、只要物体做圆周运动.在任何一个位置和状态.都满足F供=F需建立该动力关系方程是解决圆周运动问题的基本方法。
类型二圆周运动中有关连接体的临界问题
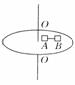 [例2]如图所示,匀速转动的水平圆盘上,放有质量均为m的小物体A、B, A、B间用细线沿半径方向相连,它们到转轴距离分别为RA=20cm,RB=30cm。A、B与盘面间的最大静摩擦力均为重力的0.4倍,试求:
[例2]如图所示,匀速转动的水平圆盘上,放有质量均为m的小物体A、B, A、B间用细线沿半径方向相连,它们到转轴距离分别为RA=20cm,RB=30cm。A、B与盘面间的最大静摩擦力均为重力的0.4倍,试求:
(1)当细线上开始出现张力时,圆盘的角速度ω0;
(2)当A开始滑动时,圆盘的角速度ω;
(3)当即将滑动时,烧断细线,A、B状态如何?
导示: (1)当细线上开始出现张力时,表明B与盘间的静摩擦力已达到最大,设此时圆盘角速度为ω0,则是kmg=mrBω02
解得: 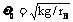 =3.7rad/s
=3.7rad/s
(2)当A开始滑动时,表明A与盘的静摩擦力也已达到最大,设此时盘转动角速度为ω,线上拉力为FT则,对A:FfAm-FT=mrAω2
对B:FfBm+FT=mrBω2
又:FfAm=FfBm=kmg
解得ω=4rad/s。
(3)烧断细线,A与盘间的静摩擦力减小,继续随盘做半径为rA=20cm的圆周运动,而B由于FfBm不足以提供必要的向心力而做离心运动。
答案:(1) 3.7rad/s (2) 4rad/s (3)A做圆周运动,B做离心运动
2、“杆模型”--管、杆的约束
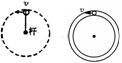 (1) 临界条件:由于轻杆或管壁的支撑,小球能到达最高点的条件是小球在最高点时速度可以为零。
(1) 临界条件:由于轻杆或管壁的支撑,小球能到达最高点的条件是小球在最高点时速度可以为零。
(2) 当0<v<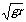 时,杆对球的作用力表现为推力,推力大小为 N=mg-m
时,杆对球的作用力表现为推力,推力大小为 N=mg-m ,N随速度增大而减小。
,N随速度增大而减小。
(3) 当v>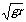 时,杆对球的作用力表现为拉力,拉力的大小为T= m
时,杆对球的作用力表现为拉力,拉力的大小为T= m -mg
-mg
[应用1](2008汕头市一中期中考试模拟)轻杆的一端固定一个质量为m的小球,以另一端o为圆心,使小球在竖直平面内做半径为r的圆周运动,则小球通过最高点时,杆对小球的作用力( )
A.可能等于零 B.可能等于mg
C.一定与小球受到的重力方向相反
D.一定随小球过最高点时速度的增大而增大
导示: 由于轻杆可以对小球提供支持力,小球通过最高点的最小速度v=O,此时支持力FN=mg;当O<v<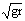 时,杆对小球的作用力为支持力,方向竖直向上,大小随小球过最高点时速度的增大而减小,取值范围为0<FN<mg;当v=
时,杆对小球的作用力为支持力,方向竖直向上,大小随小球过最高点时速度的增大而减小,取值范围为0<FN<mg;当v=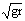 时,FN=0;当v>
时,FN=0;当v>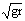 时,杆对小球的作用力为拉力,方向竖直向下,大小随小球过最高点时速度的增大而增大。故答案应为A、B。
时,杆对小球的作用力为拉力,方向竖直向下,大小随小球过最高点时速度的增大而增大。故答案应为A、B。

 解答竖直面内的圆周运动问题时,首先要搞清是绳模型还是杆模型,在最高点绳模型小球的最小速度是
解答竖直面内的圆周运动问题时,首先要搞清是绳模型还是杆模型,在最高点绳模型小球的最小速度是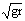 ;而杆模型小球在最高点的最小速度为零,要注意根据速度的大小判断是拉力还是支持力。
;而杆模型小球在最高点的最小速度为零,要注意根据速度的大小判断是拉力还是支持力。
知识点二物理最高点与几何最高点
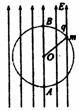
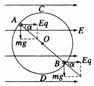 如图所示,小球在竖直平面内做圆周运动时,C为最高点,D为最低点,C点速度最小,D点速度最大。但是若加水平向右的电场E,小球带电量为+q,则在A点速度最小,在B点速度最大,小球在A点时重力与电场力的合力指向圆心,小球在B点时,重力与电场力的合力沿半径向外,这与只有重力时C、D两点的特性相似。我们把A、B两点称为物理最高点和物理最低点,而把C、D两点称为几何最高点和几何最低点。
如图所示,小球在竖直平面内做圆周运动时,C为最高点,D为最低点,C点速度最小,D点速度最大。但是若加水平向右的电场E,小球带电量为+q,则在A点速度最小,在B点速度最大,小球在A点时重力与电场力的合力指向圆心,小球在B点时,重力与电场力的合力沿半径向外,这与只有重力时C、D两点的特性相似。我们把A、B两点称为物理最高点和物理最低点,而把C、D两点称为几何最高点和几何最低点。
[应用2](淮阴中学08届高三测试卷)如图所示,细线一端系住一质量为m的小球,以另一端o为圆心,使小球在竖直面内做半径为R的圆周运动。若球带正电q,空间有竖直向上的匀强电场E,为使小球能做完整的圆周运动,在最低点A小球至少应有多大的速度?
导示: 求解本题的关键是找出带电粒子在复合场中做圆周运动的“等效最高点”以便求出小球在“等效最高点”的临界速度,进一步求出小球在最低点A的速度.
由于m、q、E的具体数值不详,故应分别讨论如下:
(1)若qE<mg,则等效重力场的方向仍向下,等效重力加速度: g′=(mg-Eq)/m.因此在最高点的临界速度vB= =
=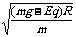
由动能定理得:mg′·2R=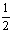 mvA2-
mvA2-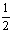 mvA2
mvA2
整理得: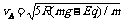
(2) 若qE>mg,则等效重力场的方向向上,等效重力加速度: g′=(Eq-mg)/m.在该等效重力场中小球轨迹“最高点”(实际为问题中的最低点--即A点)的临界速度
vB= =
=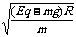
(3)若qE=mg,则等效重力场消失,小球在竖直面内做匀速圆周运动,能使小球做完整圆周运动的条件是vB >0。

 该类题的关键是求出等效重力mg′,找出等效重力场中的“等效最高点”--物理最高点,在“等效最高点”的速度v′=
该类题的关键是求出等效重力mg′,找出等效重力场中的“等效最高点”--物理最高点,在“等效最高点”的速度v′=


类型一水平面内的临界问题
 [例1]如图所示,两绳系一个质量为m=0.1 kg的小球。两绳的另一端分别固定于轴的A、B两处,上面绳长L=2 m,两绳都拉直时与轴夹角分别为300和450。问球的角速度在什么范围内,两绳始终张紧?(g取10m/s2)
[例1]如图所示,两绳系一个质量为m=0.1 kg的小球。两绳的另一端分别固定于轴的A、B两处,上面绳长L=2 m,两绳都拉直时与轴夹角分别为300和450。问球的角速度在什么范围内,两绳始终张紧?(g取10m/s2)
导示:两绳张紧时,小球受力如图所示。当ω由O逐渐增大时,ω可能出现两个临界值。
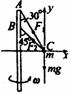 (1)BC恰好拉直,但F2仍然为零,设此时的角速
(1)BC恰好拉直,但F2仍然为零,设此时的角速
度为ω1,则有
Fx=Fsin300=mω12Lsin300
Fy=Fcos300-mg=O
代入数据得,ω1=2.40rad/s
(2)AC由拉紧转为恰好拉直,但F1已为零,设此时的角速度ω2,则有
Fx=F2sin450=mω22Lsin300
Fy=F2cos450-mg=O
代入数据得,ω2=3.16rad/s
答案:2.40rad/s≤ω≤3.16rad/s
绳系装满水的杯子在竖直平面内做圆周运动,即使到了最高点杯子中的水也不会流出,这是因为水的重力提供水做圆周运动的向心力.
(1)杯子在最高点的最小速度vmin=____.
(2)当杯子在最高点速度为v>vmin时,杯子内的水对杯底有压力,若计算中求得杯子在最高点速度v<vmin,则杯子不能到达最高点。

知识点一竖直平面内的圆周运动
竖直平面内的变速圆周运动,是典型的变速圆周运动,对于物体在竖直平面内做变速圆周运动的问题,中学物理中只研究物体通过最高点和最低点的情况,并且经常出现临界状态。
此类问题多为讨论最高点时的情况,下面具体分析几种情况:
1、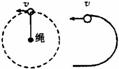 “绳模型”--外轨、绳的约束
“绳模型”--外轨、绳的约束
(1)临界条件:小球到最高点时绳子的拉力(或轨道的弹力)刚好等于零,小球的重力提供做圆周运动的向心力,
mg=mv临2/r v临=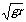
即 v临 是小球能通过最高点时的最小速度
(2)能通过最高点的条件:v≥v临
(3)不能通过最高点的条件v<v临。这种情况实际上小球在到达最高点之前就脱离了轨道
由于火车的质量比较大,火车拐弯时所需的向心力就很大.如果铁轨内外侧一样高,则外侧轮缘所受的压力很大,容易损坏;实用中使________略高于_________,从而_________和_________ 的合力提供火车拐弯时所需的向心力。
铁轨拐弯处半径为R,内外轨高度差为H,两轨间距为L,火车总质量为M,则:
(1)火车在拐弯处运动的“规定速度’’即内外轨均不受压的速度vp=_________;
(2)若火车实际速度大于vp,则___轨将受到侧向压力;
(3)若火车实际速度小于vp,则___轨将受到侧向压力。
100.(有关数列极限的题目)
(1)计算: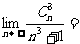 __________;
(2)计算:
__________;
(2)计算: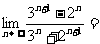 ___________;
___________;
(3)计算: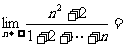 ___________;(4)若
___________;(4)若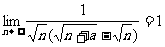 ,则常数
,则常数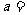 _________;
_________;
(5)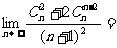 _________;
(6)数列
_________;
(6)数列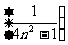 的前
的前 项和为
项和为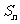 ,则
,则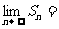 _________;
_________;
(7)若常数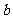 满足
满足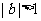 ,则
,则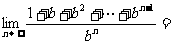 ___________;
___________;
(8)设函数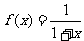 ,点
,点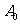 表示坐标原点,点
表示坐标原点,点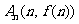 (
( 为正整数).
为正整数).
若向量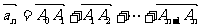 ,
,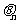 是
是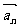 与
与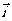 的夹角(其中
的夹角(其中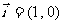 ),
),
设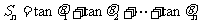 ,则
,则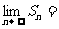 _________;
_________;
99.过抛物线 (
(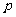 为常数且
为常数且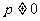 )的焦点
)的焦点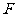 作抛物线的弦
作抛物线的弦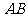 ,则
,则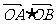 等于_________;
等于_________;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com