1．牛顿第二定律的理解：

①瞬时性：牛顿第二定律反映了力的瞬时作用效果的规律，力是产生加速度的原因，故加速度与力同时存在、同时变化、同时消失．

②矢量性：牛顿第二定律是一个矢量方程，加速度与合外力方向相同，故合外力方向就是加速度方向；反过来也有，加速度方向就是合外力方向．

③独立性：也叫做力的独立作用原理，当物体受几个力的作用时，每一个力分别产生的加速度只与此力有关，与其它力无关，这些加速度的矢量和即物体运动的加速度．

6.(★★★★★)如图9-13所示，A 、B 、C三物块质量均为m ，置于光滑水平台面上。B 、C间夹有原已完全压紧不能再压缩的弹簧，两物块用细绳相连，使弹簧不能伸展。物块A以初速度v₀沿B 、C连线方向向B运动，相碰后，A与B 、C粘合在一起，然后连接B 、C的细绳因受扰动而突然断开，弹簧伸展，从而使C与A 、B分离，脱离弹簧后C的速度为v₀ 。

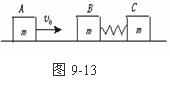(1)求弹簧所释放的势能ΔE 。

(2)若更换B 、C间的弹簧，当物块A以初速v向B运动，物块C在脱离弹簧后的速度为2v₀ ，则弹簧所释放的势能ΔE′是多少?

(3)若情况(2)中的弹簧与情况(1)中的弹簧相同，为使物块C在脱离弹簧后的速度仍为2v₀ ，A的初速度v应为多大?

5.(★★★★)(2001年上海)如图9-12(A)所示，一质量为m的物体系于长度分别为l₁ 、l₂的两根细线上，l₁的一端悬挂在天花板上，与竖直方向夹角为θ ，l₂水平拉直，物体处于平衡状态。现将l₂线剪断，求剪断瞬时物体的加速度。

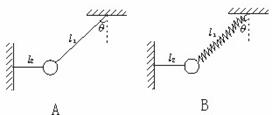
(1)下面是某同学对该题的一种解法：

解：设l₁线上拉力为T₁，l₂线上拉力为T₂，重力为mg，物体在三力作用下保持平衡：

T₁cosθ = mg ，T₁sinθ = T₂ ，T₂ = mgtanθ

剪断线的瞬间，T₂突然消失，物体即在T₂反方向获得加速度。因为mgtanθ = ma ，所以：

加速度a = gtanθ ，方向在T₂反方向。

你认为这个结果正确吗?请对该解法作出评价并说明理由。

(2)若将图A中的细线l₁改为长度相同、质量不计的轻弹簧，如图9-12(B)所示，其他条件不变，求解的步骤与(1)完全相同，即a = gtanθ ，你认为这个结果正确吗?请说明理由。

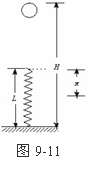
4.(★★★★)如图9-11所示，轻质弹簧原长L ，竖直固定在地面上，质量为m的小球从距地面H高处由静止开始下落，正好落在弹簧上，使弹簧的最大压缩量为x ，在下落过程中，空气阻力恒为f ，则弹簧在最短时具有的弹性势能为E_p=________。

3.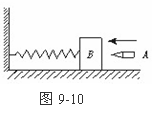(★★★)如图9-10所示的装置中，木块B与水平桌面间的接触是光滑的，子弹A沿水平方向射入木块后留在木块内，将弹簧压缩到最短。现将子弹、木块和弹簧合在一起作为研究对象(系统)，则此系统在从子弹开始射入木块到弹簧压缩至最短的整个过程中：

A、动量守恒，机械能守恒

B、动量不守恒，机械能不守恒

C、动量守恒，机械能不守恒

D、动量不守恒，机械能守恒

2.(★★★★)(2000年春)一轻质弹簧，上端悬挂于天花板，下端系一质量为M的平板，处在平衡状态。一质量为m的均匀环套在弹簧外，与平板的距离为h ，如图9-9所示。让环自由下落，撞击平板。已知碰后环与板以相同的速度向下运动，使弹簧伸长。

A、若碰撞时间极短，则碰撞过程中环与板的总动量守恒

B、若碰撞时间极短，则碰撞过程中环与板的总机械能守恒

C、环撞击板后，板的新的平衡位置与h的大小无关

D、在碰后板和环一起下落的过程中，它们减少的动能等于克服弹簧力所做的功

1.(★★★)如图9-8所示，小球在竖直力F作用下将竖直弹簧压缩，若将力F撤去，小球将向上弹起并离开弹簧，直到速度变为零为止，在小球上升的过程中：

A、小球的动能先增大后减小

B、小球在离开弹簧时动能最大

C、小球的动能最大时弹性势能为零

D、小球的动能减为零时，重力势能最大

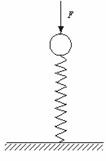
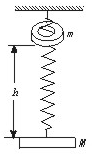
图9-8　　　　　　　　　　　　 图9-9

3.在求弹簧的弹力做功时，因该变力为线性变化，可以先求平均力，再用功的定义进行计算，也可据动能定理和功能关系：能量转化和守恒定律求解。同时要注意弹力做功的特点：W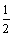_k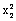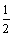=－(k－k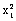)，弹力的功等于弹性势能增量的负值。弹性势能的公式E_p=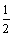kx² ，高考不作定量要求，可作定性讨论。因此，在求弹力的功或弹性势能的改变时，一般以能量的转化与守恒的角度来求解。

2.因弹簧(尤其是软质弹簧)其形变发生改变过程需要一段时间，在瞬间内形变量可以认为不变。因此，在分析瞬时变化时，可以认为弹力大小不变，即弹簧的弹力不突变。

1.弹簧的弹力是一种由形变而决定大小和方向的力.当题目中出现弹簧时，要注意弹力的大小与方向时刻要与当时的形变相对应。在题目中一般应从弹簧的形变分析入手，先确定弹簧原长位置，现长位置，找出形变量x与物体空间位置变化的几何关系，分析形变所对应的弹力大小、方向，以此来分析计算物体运动状态的可能变化。