
6、(重庆市大足中学2009年高考数学模拟试题)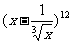 展开式中的常数项为 ( )
展开式中的常数项为 ( )
A.-1320 B.1320 C.-220 D.220
答案:C 提示: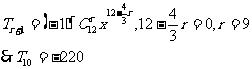
5、(上海市张堰中学高2009届第一学期期中考试)组合数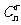
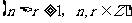 恒等于( )
恒等于( )
A、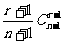 B、
B、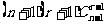 C、
C、 D、
D、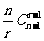 答案:D
答案:D
4、(四川省成都市高2009届高中毕业班第一次诊断性检测)(x-)9的展开式中第3项是 A、-84x3 B、84x3 C、-36x5 D、36x5 答案:D
3、(四川省成都市高2009届高中毕业班第一次诊断性检测)某学校有教职工100人,其中教师80人,职员20人,现从中选取10人组成一个考察团外出学习考察,则这10人中恰好有8名教师的不同选法种数是 A、C802C208 B、A802A208 C、A808A202 D、C808C202 答案:D
1、(四川省成都市2009届高三入学摸底测试)已知集合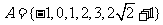 ,
, ,映射
,映射 的对应法则为
的对应法则为 .设集合
.设集合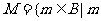 在集合
在集合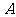 中存在原象
中存在原象 ,集合
,集合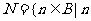 在集合
在集合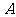 中不存在原象
中不存在原象 ,若从集合
,若从集合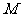 、
、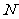 中各取一个元素组成一个对数
中各取一个元素组成一个对数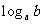 ,则组成的不同对数
,则组成的不同对数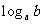 值的总个数为
值的总个数为
(A)60 (B)36 (C)13 (D) 9
答案:D
2 (湖南省长郡中学2009届高三第二次月考)在正整数数列中,由1开始依次按如下规则将某些数染成红色.先染1,再染2个偶数2、4;再染4后面最邻近的3个连续奇数5、7、9;再染9后面最邻近的4个连续偶数10、12、14、16;再染此后最邻近的5个连续奇数17、19、21、23、25.按此规则一直染下去,得到一红色子数列1,2,4,5,7,9,10,12,14,16,17,….则在这个红色子数列中,由1开始的第2003个数是 (
)
(湖南省长郡中学2009届高三第二次月考)在正整数数列中,由1开始依次按如下规则将某些数染成红色.先染1,再染2个偶数2、4;再染4后面最邻近的3个连续奇数5、7、9;再染9后面最邻近的4个连续偶数10、12、14、16;再染此后最邻近的5个连续奇数17、19、21、23、25.按此规则一直染下去,得到一红色子数列1,2,4,5,7,9,10,12,14,16,17,….则在这个红色子数列中,由1开始的第2003个数是 (
)
A 3844 B 3943 C 3945 D 4006
答案:B
6、(黑龙江省双鸭山一中2008-2009学年上学期期中考试)求圆心在直线x+y=0上,且过圆 与圆
与圆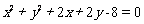 的交点的圆的方程。
的交点的圆的方程。
解:设圆的方程为
即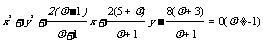
圆心
 解得
解得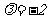
故所求圆的方程为
即
本资料由《七彩教育网》 提供!
5、(广东省华南师范附属中学2009届高三上学期第三次综合测试)已知圆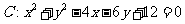 的圆心在点
的圆心在点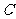 , 点
, 点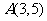 ,求;
,求;
(1)过点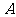 的圆的切线方程;
的圆的切线方程;
(2)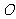 点是坐标原点,连结
点是坐标原点,连结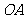 ,
,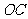 ,求
,求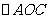 的面积
的面积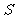 .
.
解:(1)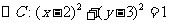 (1分)
(1分)
当切线的斜率不存在时,对直线 到直线的距离为1,满足条件(3分)
到直线的距离为1,满足条件(3分)
当 存在时,设直线
存在时,设直线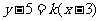 ,即
,即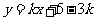 ,
,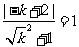
得 (5分)
(5分)
∴得直线方程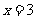 或
或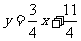 (6分)
(6分)
(2)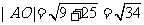 (7分)
(7分)
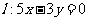 (8分)
(8分)
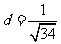 (10分)
(10分)
 (12分)
(12分)
4、(广东省恩城中学2009届高三上学期模拟考试)某公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为 元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
解:设公司在甲电视台和乙电视台做广告的时间分别为 分钟和
分钟和 分钟,总收益为
分钟,总收益为 元,
元,
 由题意得
由题意得
目标函数为 .-----------4分
.-----------4分
二元一次不等式组等价于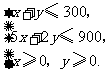
作出二元一次不等式组所表示的平面区域,即可行域.---
如图:-------------------------------8分
作直线 ,
,
即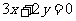 .
.
平移直线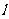 ,从图中可知,当直线
,从图中可知,当直线 过
过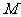 点时,目标函数取得最大值. ------10分
点时,目标函数取得最大值. ------10分
联立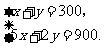 解得
解得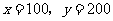 .
.
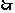 点
点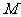 的坐标为
的坐标为 .------------------------------------12分
.------------------------------------12分
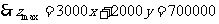 (元)-------------------------13分
(元)-------------------------13分
答:该公司在甲电视台做100分钟广告,在乙电视台做200分钟广告,公司的收益最大,最大收益是70万元.----------------------------------------------14分
3、(福建省南安一中、安溪一中、养正中学2009届高三期中联考)有三块合金,第一块合金含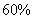 的铝和40%的铬,第二块含10%的铬和90%的钛,第三块含20%的铝,50%的铬和30%的钛。现需要由它们组合成含钛45%的新合金,试求在新的合金中,含铬的百分比范围.
的铝和40%的铬,第二块含10%的铬和90%的钛,第三块含20%的铝,50%的铬和30%的钛。现需要由它们组合成含钛45%的新合金,试求在新的合金中,含铬的百分比范围.

2、(西南师大附中高2009级第三次月考)已知圆C经过P(4,–
2),Q(– 1,3)两点,且在y轴上截得的线段长为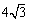 ,半径小于5.
,半径小于5.
(1)求直线PQ与圆C的方程.
(2)若直线l∥PQ,且l与圆C交于点A、B, ,求直线l的方程.
,求直线l的方程.
解:(1) PQ为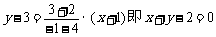 ···························································· 2分
···························································· 2分
C在PQ的中垂线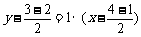 即y = x – 1上································ 3分
即y = x – 1上································ 3分
设C(n,n – 1),则 ······································· 4分
······································· 4分
由题意,有 ······································································· 5分
······································································· 5分
∴ 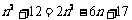 ∴
n = 1或5,r 2 = 13或37(舍)······················ 7分
∴
n = 1或5,r 2 = 13或37(舍)······················ 7分
∴圆C为 ············································································· 8分
············································································· 8分
解法二:
设所求圆的方程为
由已知得 解得
解得
当 时,
时, ;当
;当 时,
时,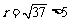 (舍)
(舍)
∴ 所求圆的方程为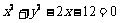
(2) 设l为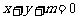 ···················································································· 9分
···················································································· 9分
由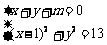 ,得
,得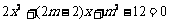 ································ 10分
································ 10分
设A(x1,y1),B(x2,y2),则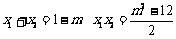 ················ 11分
················ 11分
∵
 , ∴
, ∴ 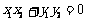 ···················································· 12分
···················································· 12分
∴
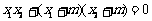
∴
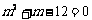 ∴ m = 3或 – 4(均满足
∴ m = 3或 – 4(均满足 )
)
∴
l为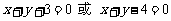 ···························································· 14分
···························································· 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com