
7、(甘肃省兰州一中2008-2009高三上学期第三次月考)一袋中装有6张同样的卡片,上面分别标出1,2,3,4,5,6,现从中随机取出3张卡片,以ξ表示取出的卡片中的最大标号。
(I)求ξ的分布列;
(II)求Eξ。
解:(I)ξ的可能取值为3,4,5,6, …………1分

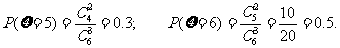 …………9分
…………9分
所以ξ的分布列为
|
ξ |
3 |
4 |
5 |
6 |
|
P |
0.05 |
0.15 |
0.3 |
0.5 |
…………10分
(II)Eξ=0.05×3+0.15×4+0.3×5+0.5×6=5.25 …………12分
6、(湖北黄陂一中2009届高三数学综合检测试题)甲,乙两人进行乒兵球比赛,在每一局比赛中,甲获胜的概率为 。
。
(1)如果甲,乙两人共比赛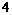 局,甲恰好负
局,甲恰好负 局的概率不大于其恰好胜
局的概率不大于其恰好胜 局的概率,试求
局的概率,试求 的取值范围;
的取值范围;
(2)若 ,当采用
,当采用 局
局 胜制的比赛规则时,求甲获胜的概率;
胜制的比赛规则时,求甲获胜的概率;
(3)如果甲,乙两人比赛 局,那么甲恰好胜
局,那么甲恰好胜 局的概率可能是
局的概率可能是 吗?
吗?
解:设每一局比赛甲获胜的概率为事件A,则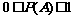
(1)由题意知 …………………………………………2分
…………………………………………2分
即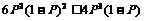 解得P=0或
解得P=0或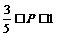 …………………………………4分
…………………………………4分
(2)甲获胜,则有比赛2局,甲全胜,或比赛3局,前2局甲胜1局,第3局甲胜,故
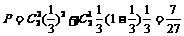 ……………………………………………………8分
……………………………………………………8分
(3)设“比赛6局,甲恰好胜3局”为事件C 则P(C)= ………9分
………9分
当P=0或P=1时,显然有 …………………………………………………10分
…………………………………………………10分
又当0<P<1时,
 …………………………11分
…………………………11分
故甲恰好胜3局的概率不可能是 .……………………………………………………12分
.……………………………………………………12分
5、(黑龙江哈尔滨三中2008年12月高三月考)袋中有3个白球,2个红球和若干个黑球(球的大小均相同),从中任取2个球,设每取得一个黑球得0分,每取得一个白球得1分,每取得一个红球得2分,已知得0分的概率为 .
.
(1)求袋中黑球的个数及得2分的概率;
(2)设所得分数为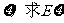 .
.
解:(1)设黑球x个,则 ,解得x=4……………………………………4分
,解得x=4……………………………………4分
 ………………………………………………………………6分
………………………………………………………………6分
(2) 可取0,1,2,3,4
可取0,1,2,3,4





 ……………………12分
……………………12分
4、(湖北省武汉市教科院2009届高三第一次调考)在某校运动会中,甲、乙、丙三支足球队进行单循环赛(即每两队比赛一场)共赛三场,每场比赛胜者得3分,负者得0分,没有平局。在每一场比赛中,甲胜乙的概率为 ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为 ;
;
(1)求甲队获第一名且丙队获第二名的概率;
(2)设在该次比赛中,甲队得分为 的分布列和数学期望。
的分布列和数学期望。
解:(1)设用队获第一且丙队获第二为事件A,则
 ………………………………………(6分)
………………………………………(6分)
(2) 可能的取值为0,3,6;则
可能的取值为0,3,6;则
甲两场皆输:
甲两场只胜一场:
 甲两场皆胜:
甲两场皆胜: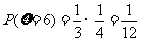
 的分布列为
的分布列为
 …………………………(12分)
…………………………(12分)
3、(湖北省武汉市教科院2009届高三第一次调考)有A、B、C、D、E共5个口袋,每个口袋装有大小和质量均相同的4个红球和2个黑球,现每次从其中一个口袋中摸出3个球,规定:若摸出的3个球恰为2个红球和1个黑球,则称为最佳摸球组合。
(1)求从口袋A中摸出的3个球为最佳摸球组合的概率;
(2)现从每个口袋中摸出3个球,求恰有3个口袋中摸出的球是最佳摸球组合的概率。
解:(1)从口袋A中摸出的3个球为最佳摸球组合即为从口袋A中摸出2个红球和1个黑球,其概率为
 ………………………………(6分)
………………………………(6分)
(2)由题意知:每个口袋中摸球为最佳组合的概率相同,从5个口袋中摸球可以看成5次独立重复试难,故所求概率为
 ……………………………………(12分)
……………………………………(12分)
1、(四川省成都市2009届高三入学摸底测试)已知甲、乙两名射击运动员各自独立地射击1次,命中10环的概率分别为、x(x>);且运动员乙在两次独立射击中恰有1次命中10环的概率为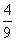 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若甲、乙两名运动员各自独立地射击1次,设两人命中10环的次数之和为随机变量 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
解:(Ⅰ)由 ,又
,又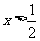 ,解得
,解得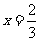 ;
;
(Ⅱ)
 |
0 |
1 |
2 |
 |
 |
 |
 |

2 (河南省实验中学2008-2009学年高三第二次月考)一个不透明的口袋内装有材质、重量、大小相同的7个小球,且每个小球的球面上要么只写有数字“08”,要么只写有文字“奥运”.假定每个小球每一次被取出的机会都相同,又知从中摸出2个球都写着“奥运”的概率是
(河南省实验中学2008-2009学年高三第二次月考)一个不透明的口袋内装有材质、重量、大小相同的7个小球,且每个小球的球面上要么只写有数字“08”,要么只写有文字“奥运”.假定每个小球每一次被取出的机会都相同,又知从中摸出2个球都写着“奥运”的概率是 。现甲、乙两个小朋友做游戏,方法是:不放回从口袋中轮流摸取一个球,甲先取、乙后取,然后甲再取,直到两个小朋友中有1人取得写着文字“奥运”的球时游戏终止,每个球在每一次被取出的机会均相同.
。现甲、乙两个小朋友做游戏,方法是:不放回从口袋中轮流摸取一个球,甲先取、乙后取,然后甲再取,直到两个小朋友中有1人取得写着文字“奥运”的球时游戏终止,每个球在每一次被取出的机会均相同.
(1)求该口袋内装有写着数字“08”的球的个数;
(2)求当游戏终止时总球次数不多于3的概率.
解(1)设该口袋内装有写着“08”的球的个数为n个。
依题意得 ,解之得n=4
,解之得n=4
所以该口袋内装有写着“08”的球的个数为4个。 ………………………6分
(2)当游戏终止时,总取球次数是1的概率等于 ,
,
当游戏终止时,总取球次数是2的概率等于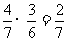 ,
,
当游戏终止时,总取球次数是3的概率等于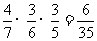 ,
,
所以,当游戏终止时,总取球次数不多于3的概率为 ……14分
……14分
10、(广东省高明一中2009届高三上学期第四次月考)一个骰子连续投2 次,点数和为4 的概率 .
答案:
本资料由《七彩教育网》 提供!
9、(广东省佛山市三水中学2009届高三上学期期中考试)某工厂生产A、B、C三种不同型号的产品,产品数量之比依次为 ,现用分层抽样的方法抽出一个容量为
,现用分层抽样的方法抽出一个容量为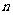 的样本,样本中A型号的产品有16件,那么此样本容量
的样本,样本中A型号的产品有16件,那么此样本容量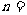 .
.
答案:72
8、(江苏省常州市2008-2009高三第一学期期中统一测试数学试题)一个靶子上有10个同心圆,半径依次为1、2、……、10,击中由内至外的区域的成绩依次为10、9、……、1环,则不考虑技术因素,射击一次,在有成绩的情况下成绩为10环的概率为 .
答案:0.01
7、(四川省成都市高中数学2009级九校联考)从0,1,2,3,5,7,11中任取3个元素分别作为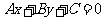 中的
中的 ,所得恰好经过原点的直线的概率为
;
,所得恰好经过原点的直线的概率为
;
答案:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com