
8、已知两个向量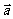 、
、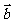 不共线,且
不共线,且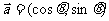 ,
, ,若
,若 ,
,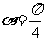 ,且
,且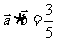 ,求
,求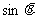 的值。
的值。
7、设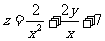 。
。
(1)若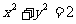 ,求
,求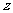 的最小值;
的最小值;
(2)若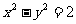 ,求
,求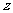 的取值范围。
的取值范围。
6、(05湖南卷)设函数f (x)的图象与直线x =a,x =b及x轴所围成图形的面积称为函数f(x)在[a,b]上的面积,已知函数y=sinnx在[0,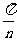 ]上的面积为
]上的面积为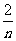 (n∈N* ),(i)y=sin3x在[0,
(n∈N* ),(i)y=sin3x在[0, ]上的面积为 ;(ii)y=sin(3x-π)+1在[
]上的面积为 ;(ii)y=sin(3x-π)+1在[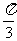 ,
, ]上的面积为
]上的面积为
5、当 时,
时,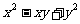 的最大值是____,最小值是____。
的最大值是____,最小值是____。
4、若函数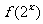 的定义域是[-1, 0],则
的定义域是[-1, 0],则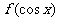 的定义域是________。
的定义域是________。
3、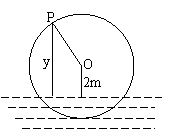 如图为一半径是3米的水轮,水轮圆心O距离水面2米,已知水轮每分钟旋转4圈,水轮上的点P到水面的距离
如图为一半径是3米的水轮,水轮圆心O距离水面2米,已知水轮每分钟旋转4圈,水轮上的点P到水面的距离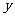 (米)与时间
(米)与时间 (秒)满足函数关系
(秒)满足函数关系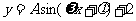 ,则有
(
)
,则有
(
)
A、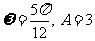 B、
B、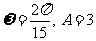
C、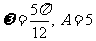 D、
D、
2、 2002年8月,在北京召开了国际数学家大会,大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的锐角为
2002年8月,在北京召开了国际数学家大会,大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的锐角为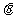 ,大正方形面积是1,小正方形的面积是
,大正方形面积是1,小正方形的面积是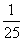 ,则
,则 的值是 ( )
的值是 ( )
A、1 B、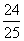 C、
C、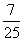 D、
D、
1、已知矩形的两相邻边长为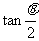 和
和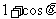 ,且对于任意实数
,且对于任意实数 ,
,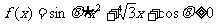 恒成立,则此矩形的面积 ( )
恒成立,则此矩形的面积 ( )
A、有最大值1,无最小值 B、有最大值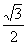 ,最小值
,最小值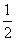
C、有最小值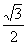 ,无最大值 D、有最大值1,最小值
,无最大值 D、有最大值1,最小值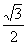
例1、求函数 的最大值和最小值.
的最大值和最小值.
例2、在平面直角坐标系中有点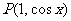 ,
,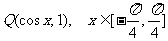 .
.
(1)求向量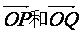 的夹角
的夹角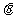 的余弦值用
的余弦值用 表示的函数
表示的函数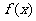 ;
;
(2)求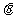 的最值.
的最值.
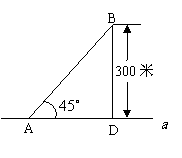
例3、如图,某海滨浴场的岸边可近似地看作直线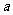 ,救生员现在岸边的A处,发现海中的B处有人求救,救生员没有直接从A处游向B处,而是沿岸边A跑到离B最近的D处,然后游向B处,若救生员在岸边的行进速度为6米/秒,在海水中的行进速度为2米/秒.
,救生员现在岸边的A处,发现海中的B处有人求救,救生员没有直接从A处游向B处,而是沿岸边A跑到离B最近的D处,然后游向B处,若救生员在岸边的行进速度为6米/秒,在海水中的行进速度为2米/秒.
(1)分析救生员的选择是否正确?
(2)在AD上找一处C,使救生员从A到B的时间最短,并求出最短时间。
例4、已知函数 。
。
(1)证明:当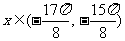 时,经过
时,经过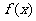 图象上的任意两点的直线的斜率恒为负数;
图象上的任意两点的直线的斜率恒为负数;
(2)设有不相等的实数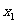 ,
, ,且
,且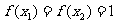 ,求
,求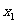 +
+ 的值。
的值。
例5、(05山东卷)已知向量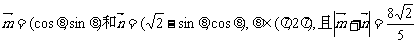 ,
,
求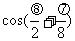 的值.
的值.
5、设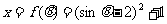 ,则
,则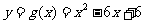 的最大值是
,最小值是
.
的最大值是
,最小值是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com