
2.玻尔的原子模型与卢瑟福的原子模型的主要区别在于,玻尔的原子模型不认为
A.原子的全部正电荷和几乎全部质量都集中在很小的区域
B.原子中的电子做加速运动时,原子一定辐射能量
C.原子中的电子从一个可能轨道跃迁到另一个可能轨道时,原子一定辐射或者吸收能量
D.原子中的电子有确定的轨道
1.放射性元素衰变时放出的三种射线,按穿透能力由强到弱的排列顺序是
A.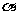 射线,
射线,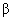 射线,
射线,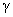 射线
射线
B.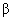 射线,
射线,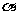 射线,
射线,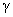 射线
射线
C.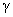 射线,
射线,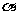 射线,
射线,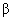 射线
射线
D.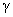 射线,
射线,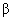 射线,
射线,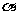 射线
射线
第I卷(48分)
20、已知函数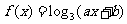 的图象经过点
的图象经过点 和
和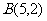 ,记
,记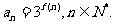
(1)求数列 的通项公式;
的通项公式;
(2)设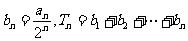 ,若
,若 ,求
,求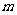 的最小值;
的最小值;
(3)求使不等式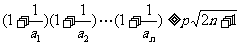 对一切
对一切 均成立的最大实数
均成立的最大实数 .
.
19.设函数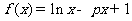
(Ⅰ)求函数 的极值点;
的极值点;
(Ⅱ)当p>0时,若对任意的x>0,恒有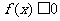 ,求p的取值范围;
,求p的取值范围;
(Ⅲ)证明: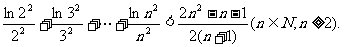
18. 设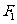 、
、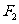 分别是椭圆
分别是椭圆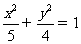 的左、右焦点.
的左、右焦点.
(Ⅰ)若P是该椭圆上的一个动点,求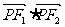 的最大值和最小值;
的最大值和最小值;
(Ⅱ)是否存在过点A(5,0)的直线l与椭圆交于不同的两点C、D,使得|F2C|=|F2D|?若存在,求直线l的方程;若不存在,请说明理由.
17.某产品具有一定的时效性,在这个时效期内,由市场调查可知,在不作广告宣传且每件获利a元的前提下,可卖出b件.若作广告宣传,广告费为n千元时比广告费为(n-1)千元时多卖出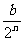 件,(n∈N*).
件,(n∈N*).
(1)试写出销售量s与n的函数关系式;
(2)当a=10,b=4000时厂家应生产多少件这种产品,做几千元广告,才能获利最大?
16.在四面体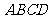 中,
中,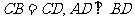 ,且
,且 分别是
分别是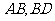 的中点,
的中点,
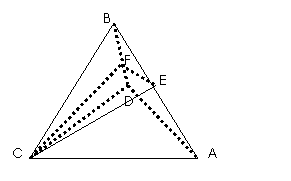 求证:(1)直线
求证:(1)直线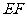 ∥面
∥面
(2)面 面
面
15、在 中,已知内角
中,已知内角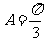 ,边
,边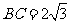 .设内角
.设内角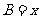 ,面积为
,面积为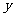 .
.
(1) 求函数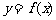 的解析式和定义域;
的解析式和定义域;
(2) 求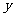 的最大值.
的最大值.
14. 若函数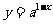
 且
且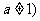 ,图象恒过定点A,又点A在直线
,图象恒过定点A,又点A在直线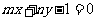 上,若
上,若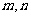 是正数,则
是正数,则 的最小值是
.
的最小值是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com