
9.①系统抽样适用于总体中的个体数较多的情况,它与简单随机抽样的联系在于:将总体均分后的每一部分进行抽样时,采用的是简单随机抽样;
②与简单随机抽样一样,系统抽样是等概率抽样,它是客观的、公平的.
③总体中的个体数恰好能被样本容量整除时,可用它们的比值作为系统抽样的间隔;当总体中的个体数不能被样本容量整除时,可用简单随机抽样先从总体中剔除少量个体,使剩下的个体数能被样本容量整除在进行系统抽样

8.系统抽样的步骤:
①采用随机的方式将总体中的个体编号 为简便起见,有时可直接采用个体所带有的号码,如考生的准考证号、街道上各户的门牌号,等等
为简便起见,有时可直接采用个体所带有的号码,如考生的准考证号、街道上各户的门牌号,等等
②为将整个的编号分段(即分成几个部分),要确定分段的间隔k 当
当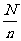 (N为总体中的个体的个数,n为样本容量)是整数时,k=
(N为总体中的个体的个数,n为样本容量)是整数时,k=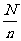 ;当
;当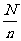 不是整数时,通过从总体中剔除一些个体使剩下的总体中个体的个数
不是整数时,通过从总体中剔除一些个体使剩下的总体中个体的个数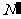 能被n整除,这时k=
能被n整除,这时k=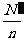 .
.
③在第一段用简单随机抽样确定起始的个体编号

④按照事先确定的规则抽取样本(通常是将 加上间隔k,得到第2个编号
加上间隔k,得到第2个编号 +k,第3个编号
+k,第3个编号 +2k,这样继续下去,直到获取整个样本)
+2k,这样继续下去,直到获取整个样本) 
7.系统抽样:当总体中的个体数较多时,可将总体分成均衡的几个部分,然后按预先定出的规则,从每一部分抽取一个个体,得到需要的样本,这种抽样叫做系统抽样.
6.简单随机抽样的特点:它是不放回抽样;它是逐个地进行抽取;它是一种等概率抽样
5.随机数表法: 随机数表抽样“三步曲”:第一步,将总体中的个体编号;第二步,选定开始的数字;第三步,获取样本号码 
4.抽签法:先将总体中的所有个体(共有N个)编号(号码可从1到N),并把号码写在形状、大小相同的号签上(号签可用小球、卡片、纸条等制作),然后将这些号签放在同一个箱子里,进行均匀搅拌,抽签时每次从中抽一个号签,连续抽取n次,就得到一个容量为n的样本 
适用范围:总体的个体数不多时 
优点:抽签法简便易行,当总体的个体数不太多时适宜采用抽签法.
3.⑴用简单随机抽样从含有N个个体的总体中抽取一个容量为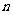 的样本时,每次抽取一个个体时任一个体被抽到的概率为
的样本时,每次抽取一个个体时任一个体被抽到的概率为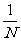 ;在整个抽样过程中各个个体被抽到的概率为
;在整个抽样过程中各个个体被抽到的概率为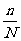 ;
;
⑵简单随机抽样的特点是,逐个抽取,且各个个体被抽到的概率相等;
⑶简单随机抽样方法,体现了抽样的客观性与公平性,是其他更复杂抽样方法的基础.
2.简单随机抽样:设一个总体的个体数为N.如果通过逐个抽取的方法从中抽取一个样本,且每次抽取时各个个体被抽到的概率相等,就称这样的抽样为简单随机抽样
1. 在统计学里,我们把所要考察对象的全体叫做总体,其中的每一个考察对象叫做个体,从总体中所抽取的一部分个体叫做总体的一个样本,样本中个体的数目叫做样本的容量.总体中所有个体的平均数叫做总体平均数,样本中所有个体的平均数叫做样本平均数.
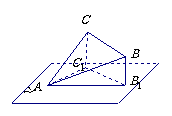 1
1 ?已知
?已知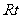
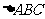 ,斜边
,斜边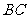 //平面
//平面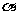 ,
,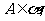
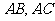 分别与平面
分别与平面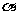 成
成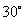 和
和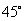 的角,已知
的角,已知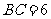 ,试求
,试求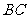 到平面
到平面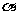 的距离
的距离
解:作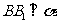 于
于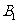 ,
,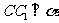 于
于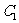 ,则由
,则由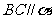 ,得
,得
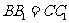 ,且
,且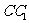 就是
就是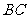 到平面
到平面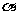 的距离,
的距离,
设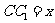 ,连结
,连结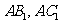 ,则
,则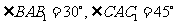 ,
,
∴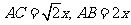 ,在
,在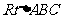 中,
中,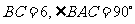 ,
,
∴ ,∴
,∴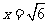 ,即
,即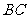 到平面
到平面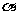 的距离为
的距离为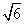 .
.
2.已知棱长为a的正方体ABCD-A1B1C1D1,M、N分别是B1C1和C1D1的中点.
⑴求证:B1D1//平面CMN.
⑵求点B1到平面CMN的距离.
分析:显然有B1D1//MN,所以B1D1//平面CMN.
∴ 点B1到平面CMN的距离就是直线B1D1到平面CMN的距离.
∴ 可以考虑求B1D1的中点O到平面CMN的距离.
解:⑴∵ M、N分别是B1C1和C1D1的中点,∴ MN//B1D1.
而 MN 平面CMN,B1D1
平面CMN,B1D1 平面CMN,
平面CMN, ∴ B1D1//平面CMN.
∴ B1D1//平面CMN.
⑵连接AC、A1C1,A1C1交B1D1于O,交MN于E,则E是MN的中点,且MN⊥A1C1.
∵ AA1⊥平面A1B1C1D1,MN  平面CMN,
平面CMN,
∴ AA1⊥MN.
∴ MN⊥平面A1ACC1.
∴ 平面CMN⊥平面A1ACC1.
在平面A1ACC1内作OH垂直于平面CMN和平面A1ACC1的交线CE于H,则OH⊥平面CMN.
∴ OH的长就是点O到平面CMN的距离.
由⑴知,OH的长就是点B1到平面CMN的距离.
由Rt△OHE∽Rt△CC1E可得,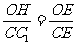 .
.
∵ 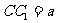 ,
,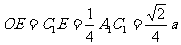 ,
,
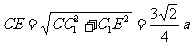 ,
,
∴ 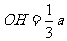 .
.
∴ 点B1到平面CMN的距离等于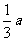 .
.
说明:①由于点B1在平面CMN内的射影不易作出,所以我们就把点B1平移到点O,作出点O在平面CMN内的射影H,从而求出点B1到平面CMN的距离,这是处理点到平面的距离问题的常用手段.
②对于直线到平面的距离问题,一般取直线上的特殊点向平面上做垂线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com