
3. 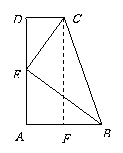 证明: 过点C作CF⊥AB,垂足为F.……………… 1分
证明: 过点C作CF⊥AB,垂足为F.……………… 1分
∵ 在梯形ABCD中,AB∥CD,∠A=90°,
∴ ∠D=∠A=∠CFA=90°.
∴四边形AFCD是矩形.
AD=CF, BF=AB-AF=1.……………………………… 3分
在Rt△BCF中,
CF2=BC2-BF2=8,
∴ CF=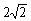 .
.
∴ AD=CF=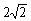 .………………………………………………………… 5分
.………………………………………………………… 5分
∵ E是AD中点,
∴ DE=AE=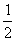 AD=
AD=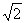 .……………………………………………… 6分
.……………………………………………… 6分
在Rt△ABE和 Rt△DEC中,
EB2=AE2+AB2=6,
EC2= DE2+CD2=3,
EB2+ EC2=9=BC2.
∴ ∠CEB=90°.……………………………………………………… 9分
∴ EB⊥EC. …………………………………………………………… 10分
2. 解:正确。
证明如下:
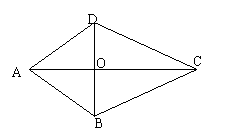 方法一:设AC,BD交于O,∵AB=AD,BC=DC,AC=AC,
方法一:设AC,BD交于O,∵AB=AD,BC=DC,AC=AC,
∴△ABC≌△ADE,
∴∠BAC=∠DAC
AB=AD,∴AO⊥BD
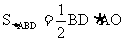 ,
,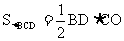
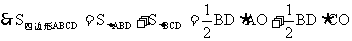
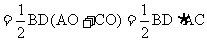
方法二:∵AB=AD,
∴点A在线段BD的中垂线上。
又∵CB=CD,∴点C与在线段BD的中垂线上,
∴AC所在的直线是线段BD的中垂线,即BD⊥AC;
设AC,BD交于O,∵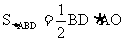 ,
,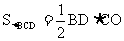
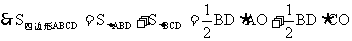
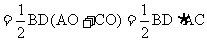
1. 证明:(1)∵四边形ABCD是菱形,
∴AB=AD,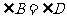 ,
,
又∵BE=DF
∴ ≌
≌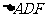
∴AE=AF
(2)连接AC
∵AB=BC,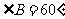
∴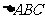 是等边三角形,
是等边三角形,
E是BC的中点
∴AE⊥BC, ∴ ,同理
,同理
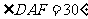
∵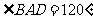
∴
又∵AE=AF
∴ 是等边三角形。
是等边三角形。
1.32;.2. (1)2 (2)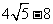 ;3.
;3. 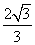 ;4.
;4.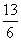 ;5. 4或9或15个小正方形;6.
;5. 4或9或15个小正方形;6. 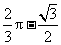 ;7. 3 ;8.
;7. 3 ;8.
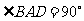 (或
(或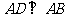 ,
, 等);9.
等);9.  或
或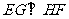 或
或 等(任填一个满足题意的均可);10.
等(任填一个满足题意的均可);10. 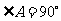 或
或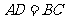 或
或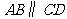 ;11. 9;12. 7;13.
;11. 9;12. 7;13. 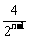 ;14.
;14.  ;15.
;15. 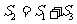 ;16.
;16. 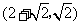 ;17. 8cm;18. 60;19. 22.5 20. ③;21.
;17. 8cm;18. 60;19. 22.5 20. ③;21. 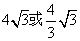 ;22. 5;23. 0.6;24. 平行四边形(或矩形或菱形);25.14;26. 2或
;22. 5;23. 0.6;24. 平行四边形(或矩形或菱形);25.14;26. 2或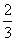 ;27.20;28.48;29.15;30.6;
;27.20;28.48;29.15;30.6;
1.C 2.D 3.D 4.B 5.C 6.A 7.A 8.B 9.C 10.A 11.C 12.A 13.C 14.B 15.B 16.D 17.D 18.A 19.C 20.B 21.D 22.D 23.A 24.A
38.(2008年上海市)如图11,已知平行四边形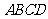 中,对角线
中,对角线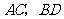 交于点
交于点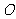 ,
,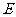 是
是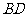 延长线上的点,且
延长线上的点,且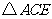 是等边三角形.
是等边三角形.
 (1)求证:四边形
(1)求证:四边形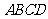 是菱形;
是菱形;
(2)若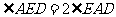 ,求证:四边形
,求证:四边形 是正方形.
是正方形.
特殊平行四边形答案
36.(2008湖南益阳市) △ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.
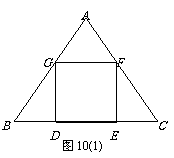 Ⅰ.证明:△BDG≌△CEF;
Ⅰ.证明:△BDG≌△CEF;
Ⅱ. 探究:怎样在铁片上准确地画出正方形.
小聪和小明各给出了一种想法,请你在Ⅱa和Ⅱb的两个问题中选择一个你喜欢的问题解答. 如果两题都解,只以Ⅱa的解答记分.
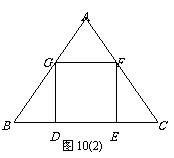
Ⅱa. 小聪想:要画出正方形DEFG,只要能计算出正方形的边长就能求出BD和CE的长,从而确定D点和E点,再画正方形DEFG就容易了.
设△ABC的边长为2 ,请你帮小聪求出正方形的边长(结果用含根号的式子表示,不要求分母有理化) .
Ⅱb. 小明想:不求正方形的边长也能画出正方形. 具体作法是:
①在AB边上任取一点G’,如图作正方形G’D’E’F’;
②连结BF’并延长交AC于F;
③作FE∥F’E’交BC于E,FG∥F′G′交AB于G,GD∥G’D’交BC于D,则四边形DEFG即为所求.
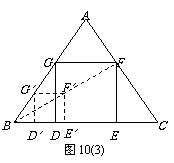 你认为小明的作法正确吗?说明理由.
你认为小明的作法正确吗?说明理由.
35. (2008广州市)如图7,在菱形ABCD中,∠DAB=60°,过点C作CE⊥AC且与AB的延长线交于点E,求证:四边形AECD是等腰梯形
(2008广州市)如图7,在菱形ABCD中,∠DAB=60°,过点C作CE⊥AC且与AB的延长线交于点E,求证:四边形AECD是等腰梯形
|
34.(2008广东肇庆市)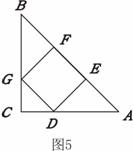 如图5,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.
如图5,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.
(1)求证AE=BF;
(2)若BC=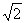 cm,求正方形DEFG的边长.
cm,求正方形DEFG的边长.
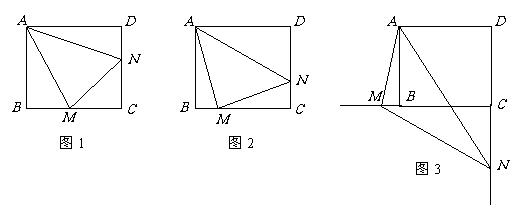
33. (2008黑龙江黑河)已知:正方形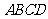 中,
中,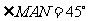 ,
,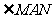 绕点
绕点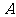 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交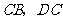 (或它们的延长线)于点
(或它们的延长线)于点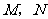 .
.
当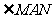 绕点
绕点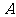 旋转到
旋转到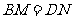 时(如图1),易证
时(如图1),易证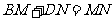 .
.
(1)当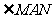 绕点
绕点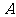 旋转到
旋转到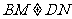 时(如图2),线段
时(如图2),线段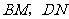 和
和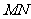 之间有怎样的数量关系?写出猜想,并加以证明.
之间有怎样的数量关系?写出猜想,并加以证明.
(2)当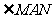 绕点
绕点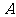 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段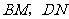 和
和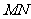 之间又有怎样的数量关系?请直接写出你的猜想.
之间又有怎样的数量关系?请直接写出你的猜想.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com