
23. (1)当E为CD中点时,EB平分∠AEC。………………………1分
由∠D=900 ,DE=1,AD=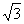 ,推得DEA=600,同理,∠CEB=600 ,从而∠AEB=∠CEB=600 ,即EB平分∠AEC。……………………………3分
,推得DEA=600,同理,∠CEB=600 ,从而∠AEB=∠CEB=600 ,即EB平分∠AEC。……………………………3分
(2)①∵CE∥BF,∴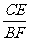 =
=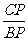 =
=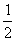 ∴BF=2CE。…………………5分
∴BF=2CE。…………………5分
∵AB=2CE,∴点B平分线段AF………………………………………6分
②能。……………………………………………………………………7分
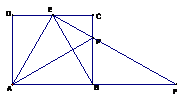 证明:∵CP=
证明:∵CP=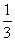
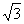 ,CE=1,∠C=900 ,∴EP=
,CE=1,∠C=900 ,∴EP=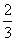
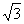 。
。
在Rt △ADE中,AE= 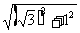 =2,∴AE=BF,
=2,∴AE=BF,
又∵PB=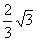 ,∴PB=PE
,∴PB=PE
∵∠AEP=∠BP=900 ,∴△PAS≌△PFB。…………………………9分
∴△PAE可以△PFB按照顺时针方向绕P点旋转而得到。
旋转度数为1200 且是 …………………………………………………10分
22. 解:(1) 内. 2分
(2) 证法一:连接CD, 3分
∵ DE∥AC,DF∥BC,
∴ 四边形DECF为平行四边形, 4分
又∵ 点D是△ABC的内心,
∴ CD平分∠ACB,即∠FCD=∠ECD, 5分
又∠FDC=∠ECD,∴ ∠FCD=∠FDC
∴ FC=FD, 6分
∴ □DECF为菱形. 7分
证法二:
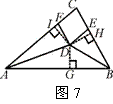 过D分别作DG⊥AB于G,DH⊥BC于H,DI⊥AC于I. 3分
过D分别作DG⊥AB于G,DH⊥BC于H,DI⊥AC于I. 3分
∵AD、BD分别平分∠CAB、∠ABC,
∴DI=DG,
DG=DH.
∴DH=DI. 4分
∵DE∥AC,DF∥BC,
∴四边形DECF为平行四边形, 5分
∴S□DECF=CE·DH =CF·DI,
∴CE=CF. 6分
∴□DECF为菱形. 7分
21. 证明:在正方形ABCD中,取AB=2
∵N为BC的中点,
∴NC=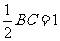
在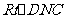 中,
中,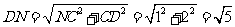
又∵NE=ND,
∴CE=NE-NC=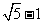 ,
,
 ,
,
故矩形DCEF为黄金矩形。
20. 解:(1)BG=DE
∵四边形ABCD和四边形CEFG都是正方形,
∴GC=CE,BC=CD,∠BCG=∠DCE=90°)
∴△BCG≌△DCE
∴BG=DE
(2)存在. △BCG和△DCE
△BCG绕点C顺时针方向旋转90°与△DCE重合
19. 解:解:当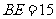 cm时,
cm时,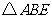 的面积是
的面积是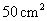 ;
;
当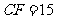 cm时,
cm时,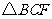 的面积是
的面积是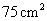 ;
;
当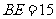 cm时,
cm时,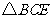 的面积是
的面积是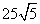
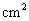 .
.
(每种情况,图给1分,计算结果正确1分,共6
18. 解:(1)连结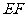 交
交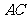 于
于 ,
,
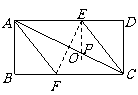 当顶点
当顶点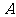 与
与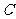 重合时,折痕
重合时,折痕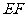 垂直平分
垂直平分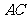 ,
,
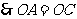 ,
,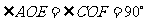 1分
1分
 在平行四边形
在平行四边形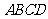 中,
中,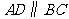 ,
,
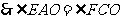 ,
,
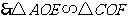 .
.
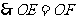 2分
2分
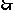 四边形
四边形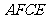 是菱形. 3分
是菱形. 3分
(2)四边形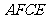 是菱形,
是菱形,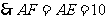 .
.
设 ,
,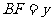 ,
,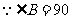 ,
,
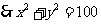 4分
4分
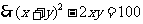 ①
①
又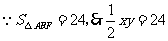 ,则
,则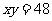 . ② 5分
. ② 5分
由①、②得: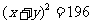 6分
6分
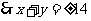 ,
,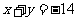 (不合题意舍去)
(不合题意舍去)
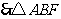 的周长为
的周长为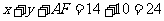 . 7分
. 7分
(3)过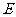 作
作 交
交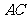 于
于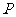 ,则
,则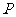 就是所求的点. 9分
就是所求的点. 9分
证明:由作法, ,
,
由(1)得: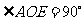 ,又
,又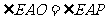 ,
,
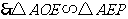 ,
,
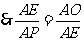 ,则
,则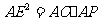 10分
10分
 四边形
四边形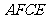 是菱形,
是菱形,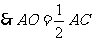 ,
,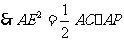 . 11分
. 11分
 12分
12分
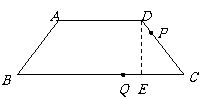
17.结论均是PA2+PC2=PB2+PD2(图2 2分,图3 1分)
证明:如图2过点P作MN⊥AD于点M,交BC于点N,
因为AD∥BC,MN⊥AD,所以MN⊥BC
在Rt△AMP中,PA2=PM2+MA2
在Rt△BNP中,PB2=PN2+BN2
在Rt△DMP中,PD2=DM2+PM2
在Rt△CNP中,PC2=PN2+NC2
所以PA2+PC2=PM2+MA2+PN2+NC2
PB2+PD2=PM2+DM2+BN2+PN2
因为MN⊥AD,MN⊥NC,DC⊥BC,所以四边形MNCD是矩形
所以MD=NC,同理AM = BN,
所以PM2+MA2+PN2+NC2=PM2+DM2+BN2+PN2
即PA2+PC2=PB2+PD2
16. 解(1)证明: ∵CE平分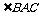 ,∴
,∴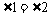 ,
,
又∵MN∥BC,∴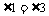 ,∴
,∴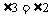 ,∴
,∴ .
.
同理,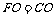 .∴
.∴
 .
.
(2)当点O运动到AC的中点时,四边形AECF是矩形.
∵ ,点O是AC的中点.∴四边形AECF是平行四边形.
,点O是AC的中点.∴四边形AECF是平行四边形.
又∵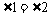 ,
,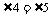 .∴
.∴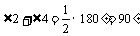 ,即
,即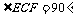 .∴四边形AECF是矩形.
.∴四边形AECF是矩形.
15. 证明:(1)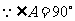 ,
,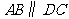 ,
, .
.
由沿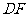 折叠后
折叠后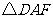 与
与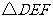 重合,知
重合,知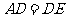 ,
,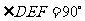 .
.
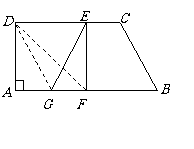
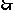 四边形
四边形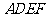 是矩形,且邻边
是矩形,且邻边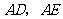 相等.
相等.
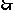 四边形
四边形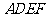 是正方形. 3分
是正方形. 3分
(2)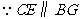 ,且
,且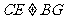 ,
,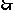 四边形
四边形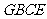 是梯形. 4分
是梯形. 4分
 四边形
四边形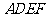 是正方形,
是正方形,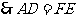 ,
,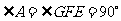 .
.
又点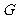 为
为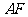 的中点,
的中点,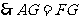 .连接
.连接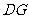 .
.
在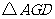 与
与 中,
中,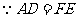 ,
,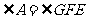 ,
,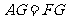 ,
,
 ,
,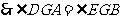 . 6分
. 6分
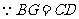 ,
,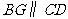 ,
,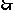 四边形
四边形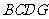 是平行四边形.
是平行四边形.
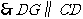 .
.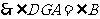 .
.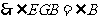 .
.
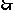 四边形
四边形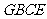 是等腰梯形. 8分
是等腰梯形. 8分
注:第(2)小题也可过点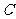 作
作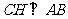 ,垂足为点
,垂足为点 ,证
,证
14. 解:(1)36;(2)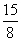 秒;
秒;
(3)当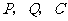 三点构成直角三角形时,有两种情况:
三点构成直角三角形时,有两种情况:
①当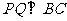 时,设
时,设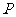 点离开
点离开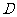 点
点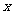 秒,
秒,
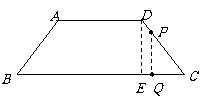 作
作 于
于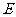 ,
,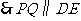 .
.
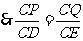 ,
,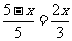 ,
,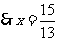 .
.
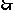 当
当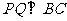 时,
时,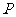 点离开
点离开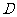 点
点 秒.
秒.
②当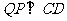 时,设
时,设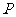 点离开
点离开 点
点 秒,
秒,
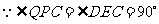 ,
,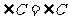 .
.
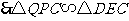 .
.
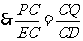 .
.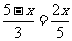 .
.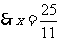 .
.
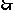 当
当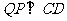 时,点
时,点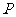 离开点
离开点
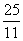 秒.
秒.
由①②知,当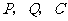 三点构成直角三角形时,点
三点构成直角三角形时,点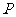 离开点
离开点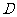
 秒或
秒或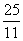 秒.
秒.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com