
33. 解:(1)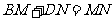 成立.
成立.
 如图,把
如图,把 绕点
绕点 顺时针
顺时针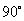 ,得到
,得到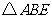 ,
,
则可证得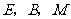 三点共线(图形画正确)
三点共线(图形画正确)
证明过程中,
证得: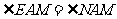
证得: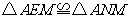
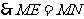
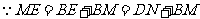
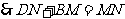
(2)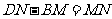
32. 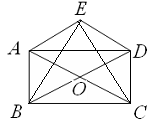 (1)解:四边形AODE是菱形;
(1)解:四边形AODE是菱形;
(2)证明:∵四边形AODE是菱形
∴AE=ED
∴∠EAD=∠EDA
∵四边形ABCD是矩形
∴∠BAD=∠CDA,AB=CD
∴∠BAD+∠EAD=∠CDA+∠EDA
即:∠BAE=∠CDE
∴△BAE≌△CDE
∴EB=EC
31. 解:填“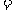 ”
”
理由: 四边形
四边形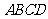 是平行四边形
是平行四边形
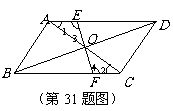
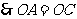 ,
, 3分
3分
 ,
,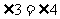 4分
4分
在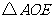 和
和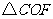 中
中
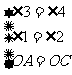
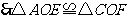 . 5分
. 5分
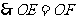 6分
6分
30. 解:过点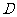 作
作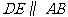 交
交 于点
于点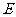 ,
,
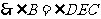 , 1分
, 1分
又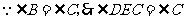 ,
,
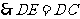 . 3分
. 3分
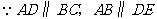 ,
,
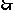 四边形
四边形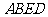 为平行四边形, 5分
为平行四边形, 5分
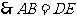 ,
,
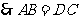 .(答案不唯一) 6分
.(答案不唯一) 6分
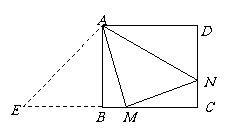
29.  解:(1)证明:∵∠A=90°
∠ABE=30° ∠AEB=60°
解:(1)证明:∵∠A=90°
∠ABE=30° ∠AEB=60°
∵EB=ED ∴∠EBD=∠EDB=30°
∵PQ∥BD ∴∠EQP=∠EBD ∠EPQ=∠EDB
∴∠EPQ=∠EQP=30° ∴EQ=EP ………………1分
过点E作EM⊥OP垂足为M ∴PQ=2PM
∵∠EPM=30°∴PM=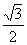 PE ∴PE=
PE ∴PE=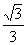 PQ………1分
PQ………1分
∵BE=DE=PD+PE ∴BE=PD+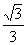 PQ………………1分
PQ………………1分
 (2)解:由题意知AE=
(2)解:由题意知AE=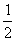 BE ∴DE=BE=2AE
BE ∴DE=BE=2AE
∵AD=BC=6 ∴AE=2 DE=BE=4 …………1分
当点P在线段ED上时(如图1)
过点Q做QH⊥AD于点H QH=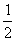 PQ=
PQ=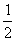 x
x
由(1)得PD=BE-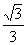 PQ=4-
PQ=4-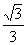 x
x
∴y=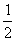 PD·QH=
PD·QH=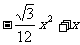 ………………1分
………………1分
当点P在线段ED的延长线上时(如图2)过点Q作QH⊥DA交DA延长线于点H’ ∴QH’=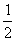 x
x
过点E作EM’⊥PQ于点M’ 同理可得EP=EQ=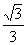 PQ ∴BE=
PQ ∴BE=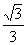 PQ-PD
PQ-PD
∴PD=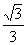 x-4 y=
x-4 y=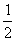 PD·QH’=
PD·QH’=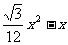 ……………………1分
……………………1分
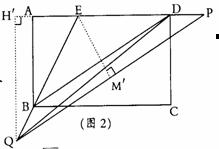
(3)解:连接PC交BD于点N(如图3)∵点P是线段ED中点
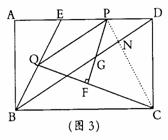 ∴EP=PD=2 ∴PQ=
∴EP=PD=2 ∴PQ=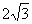 ∵DC=AB=AE·tan60°=
∵DC=AB=AE·tan60°=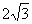
∴PC=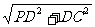 =4 ∴cos∠DPC=
=4 ∴cos∠DPC=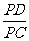 =
=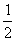 ∴∠DPC=60°
∴∠DPC=60°
∴∠QPC=180°-∠EPQ-∠DPC=90°…………………………1分
∵PQ∥BD ∴∠PND=∠QPC=90°
∴PN=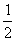 PD=1……………1分
PD=1……………1分
QC=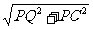 =
=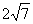 ∵∠PGN=90°-∠FPC ∠PCF=90°-∠FPC
∵∠PGN=90°-∠FPC ∠PCF=90°-∠FPC
∴∠PCN=∠PCF……………1分 ∵∠PNG=∠QPC=90° ∴△PNG-△QPC
∴ ∴PG=
∴PG=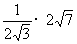 =
=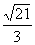 …………………………1分
…………………………1分
28. 解:∵四边形ABCD是正方形,
∴ AD=CD ,∠A=∠DCF=900
又∵DF⊥DE,
∴∠1+∠3=∠2+∠3
∴∠1=∠2
在Rt△DAE和Rt△DCE中,
∠1=∠2
AD=CD
∠A=∠DCF
∴Rt△DAE Rt△DCE
Rt△DCE
∴DE=DF.
27. 解:21.(1)在平行四边形ABCD中,∠A=∠C,AD=CB,AB=CD.
∵E,F分别为AB,CD的中点
∴AE=CF
在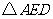 和
和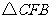 中,
中,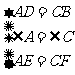
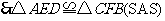 .
.
(2)若AD⊥BD,则四边形BFDE是菱形.
证明: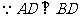 ,
,
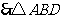 是
是 ,且
,且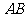 是斜边(或
是斜边(或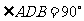 )
)
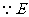 是
是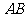 的中点,
的中点,
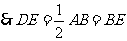 .
.
由题意可知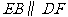 且
且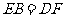 ,
,
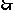 四边形
四边形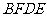 是平行四边形,
是平行四边形,
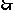 四边形
四边形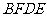 是菱形.
是菱形.
26. (1)证明:∵AE∥BD, ∴∠E=∠BDC
∵DB平分∠ADC ∴∠ADC=2∠BDC
又∵∠C=2∠E
∴∠ADC=∠BCD
∴梯形ABCD是等腰梯形
(2)解:由第(1)问,得∠C=2∠E=2∠BDC=60°,且BC=AD=5
∵ 在△BCD中,∠C=60°, ∠BDC=30°
∴∠DBC=90°
∴DC=2BC=10
25. 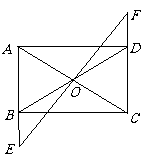 (1)证明:
(1)证明: 四边形
四边形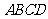 是矩形,
是矩形,
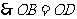 (矩形的对角线互相平分),
(矩形的对角线互相平分),
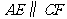 (矩形的对边平行).
(矩形的对边平行).
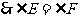 ,
,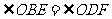 .
.
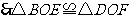 (A.A.S).
(A.A.S).
(2)当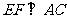 时,四边形
时,四边形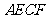 是菱形.
是菱形.
证明: 四边形
四边形 是矩形,
是矩形,
 (矩形的对角线互相平分).
(矩形的对角线互相平分).
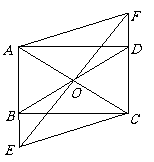 又由(1)
又由(1)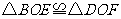 得,
得,
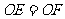 ,
,
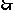 四边形
四边形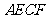 是平行四边形(对角线互相平分的
是平行四边形(对角线互相平分的
四边形是平行四边形)
又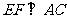 ,
,
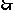 四边形
四边形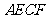 是菱形(对角线互相垂直的平行四
是菱形(对角线互相垂直的平行四
边形是菱形).
24. (1)四边形BECF是菱形。·
证明:EF垂直平分BC,
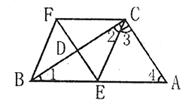 ∴BF=FC,BE=EC,∴∠1=∠2
∴BF=FC,BE=EC,∴∠1=∠2
∵∠ACB=90°
∴∠1+∠4=90°
∠3+∠2=90°
∴∠3=∠4
∴EC=AE
∴BE=AE
∵CF=AE
∴BE=EC=CF=BF
∴四边形BECF是菱形
(2)当∠A=45。时,菱形BESF是正方形
证明:∵∠A=45。, ∠ACB=90。
∴∠1=45。
∴∠EBF=2∠A=90。
∴菱形BECF是正方形
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com