
将各个选择项逐一代入题设进行检验,从而获得正确判断的方法叫代入法,又称为验证法,即将各选择支分别作为条件,去验证命题,能使命题成立的选择支就是应选的答案。
[例8](97年高考题)函数y=sin( -2x)+sin2x的最小正周期是_____。
-2x)+sin2x的最小正周期是_____。
A.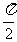 B.
B.  C. 2
C. 2 D. 4
D. 4
[解]代入法:f(x+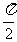 )=sin[
)=sin[ -2(x+
-2(x+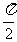 )]+sin[2(x+
)]+sin[2(x+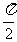 )]=-f(x),而
)]=-f(x),而
f(x+π)=sin[ -2(x+π)]+sin[2(x+π)]=f(x)。所以应选B;
-2(x+π)]+sin[2(x+π)]=f(x)。所以应选B;
[另解]直接法:y=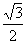 cos2x-
cos2x-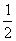 sin2x+sin2x=sin(2x+
sin2x+sin2x=sin(2x+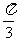 ),T=π,选B。
),T=π,选B。
[例9](96年高考题)母线长为1的圆锥体积最大时,其侧面展开图的圆心角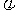 等于_____。
等于_____。
A. 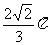 B.
B.
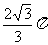 C.
C. 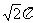 D.
D.
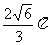
[解]代入法:四个选项依次代入求得r分别为: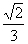 、
、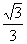 、
、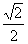 、
、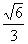 ,再求得h分别为:
,再求得h分别为: 、
、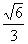 、
、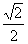 、
、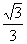 ,最后计算体积取最大者,选D。
,最后计算体积取最大者,选D。
[另解]直接法:设底面半径r,则V=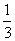 πr
πr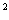
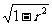 =
=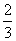 π
π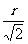
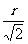
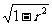 ≤…
≤…
其中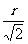 =
=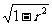 ,得到r=
,得到r=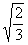 ,所以
,所以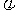 =2π
=2π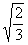 /1=
/1=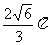 ,选D。
,选D。
代入法适应于题设复杂,结论简单的选择题。若能据题意确定代入顺序,则能较大提高解题速度。
从题设条件出发,运用定理、性质、公式推演,根据“四选一”的指令,逐步剔除干扰项,从而得出正确判断的方法叫筛选法或剔除法。
[例6](95年高考题)已知y=log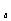 (2-ax)在[0,1]上是x的减函数,则a的取值范围是_____。
(2-ax)在[0,1]上是x的减函数,则a的取值范围是_____。
A. [0,1] B. (1,2] C. (0,2) D. [2,+∞)
[解]∵ 2-ax是在[0,1]上是减函数,所以a>1,排除答案A、C;若a=2,由2-ax>0得x<1,这与[0,1]不符合,排除答案C。所以选B。
[例7](88年高考题)过抛物线y =4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是______。
=4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是______。
A. y =2x-1 B. y
=2x-1 B. y =2x-2 C. y
=2x-2 C. y =-2x+1 D. y
=-2x+1 D. y =-2x+2
=-2x+2
[解]筛选法:由已知可知轨迹曲线的顶点为(1,0),开口向右,由此排除答案A、C、D,所以选B;
[另解]直接法:设过焦点的直线y=k(x-1),则 ,消y得:
,消y得:
k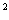 x
x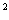 -2(k
-2(k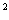 +2)x+k
+2)x+k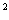 =0,中点坐标有
=0,中点坐标有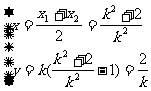 ,消k得y
,消k得y =2x-2,选B。
=2x-2,选B。
筛选法适应于定性型或不易直接求解的选择题。当题目中的条件多于一个时,先根据某些条件在选择支中找出明显与之矛盾的,予以否定,再根据另一些条件在缩小的选择支的范围那找出矛盾,这样逐步筛选,直到得出正确的选择。它与特例法、图解法等结合使用是解选择题的常用方法,近几年高考选择题中约占40%。
用特殊值(特殊图形、特殊位置)代替题设普遍条件,得出特殊结论,对各个选项进行检验,从而作出正确判断的方法叫特例法。常用的特例有特殊数值、特殊数列、特殊函数、特殊图形、特殊角、特殊位置等。
[例4](97年高考题)定义在区间(-∞,∞)的奇函数f(x)为增函数,偶函数g(x)在区间[0,+∞)的图象与f(x)的图象重合,设a>b>0,给出下列不等式①f(b)-f(-a)>g(a)-g(-b);②f(b)-f(-a)<g(a)-g(-b);③f(a)-f(-b)>g(b)-g(-a);④f(a)-f(-b)<g(b)-g(-a).其中成立的是( )
A. ①与④ B. ②与③ C. ①与③ D. ②与④
[解]令f(x)=x,g(x)=|x|,a=2,b=1,则:f(b)-f(-a)=1-(-2)=3, g(a)-g(-b)=2-1=1,得到①式正确;f(a)-f(-b)=2-(-1)=3, g(b)-g(-a)=1-2=-1,得到③式正确。所以选C。
[另解]直接法:f(b)-f(-a)=f(b)+f(a),g(a)-g(-b)=g(a)-g(b)=f(a)-f(b),从而①式正确;f(a)-f(-b)=f(a)+f(b),g(b)-g(-a)=g(b)-g(a)=f(b)-f(a),从而③式正确。所以选C。
[例5](85年高考题)如果n是正偶数,则C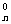 +C
+C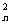 +…+C
+…+C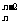 +C
+C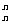 =______。
=______。
A. 2 B. 2
B. 2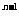 C. 2
C. 2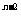 D. (n-1)2
D. (n-1)2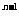
[解]用特值法:当n=2时,代入得C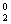 +C
+C =2,排除答案A、C;当n=4时,代入得C
=2,排除答案A、C;当n=4时,代入得C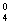 +C
+C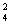 +C
+C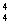 =8,排除答案D。所以选B。
=8,排除答案D。所以选B。
[另解]直接法:由二项展开式系数的性质有C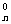 +C
+C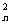 +…+C
+…+C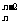 +C
+C =2
=2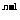 ,选B。
,选B。
当正确的选择对象,在题设普遍条件下都成立的情况下,用特殊值(取得愈简单愈好)进行探求,从而清晰、快捷地得到正确的答案,即通过对特殊情况的研究来判断一般规律,是解答本类选择题的最佳策略。近几年高考选择题中可用或结合特例法解答的约占30%左右。
直接从题设条件出发,运用有关概念、性质、定理、法则等知识,通过推理运算,得出结论,再对照选择项,从中选正确答案的方法叫直接法。
[例1](96年高考题)若sin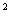 x>cos
x>cos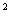 x,则x的取值范围是______。
x,则x的取值范围是______。
A.{x|2k -
-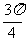 <x<2k
<x<2k +
+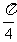 ,k
,k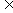 Z} B.
{x|2k
Z} B.
{x|2k +
+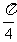 <x<2k
<x<2k +
+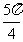 ,k
,k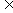 Z}
Z}
C. {x|k -
-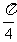 <x<k
<x<k +
+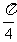 ,k
,k Z} D. {x|k
Z} D. {x|k +
+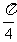 <x<k
<x<k +
+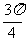 ,k
,k Z}
Z}
[解]直接解三角不等式:由sin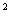 x>cos
x>cos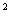 x得cos
x得cos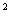 x-sin
x-sin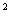 x<0,即cos2x<0,所以:
x<0,即cos2x<0,所以:
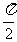 +2kπ<2x<
+2kπ<2x<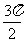 +2kπ,选D;
+2kπ,选D;
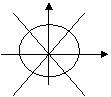
[另解]数形结合法:由已知得|sinx|>|cosx|,画出单位圆:
利用三角函数线,可知选D。
[例2](96年高考题)设f(x)是(-∞,∞)是的奇函数,f(x+2)=-f(x),当0≤x≤1时,f(x)=x,则f(7.5)等于______。
A. 0.5 B. -0.5 C. 1.5 D. -1.5
[解]由f(x+2)=-f(x)得f(7.5)=-f(5.5)=f(3.5)=-f(1.5)=f(-0.5),由f(x)是奇函数得f(-0.5)=-f(0.5)=-0.5,所以选B。
也可由f(x+2)=-f(x),得到周期T=4,所以f(7.5)=f(-0.5)=-f(0.5)=-0.5。
[例3](87年高考题)七人并排站成一行,如果甲、乙两人必需不相邻,那么不同的排法的种数是_____。
A. 1440 B. 3600 C. 4320 D. 4800
[解一]用排除法:七人并排站成一行,总的排法有P 种,其中甲、乙两人相邻的排法有2×P
种,其中甲、乙两人相邻的排法有2×P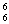 种。因此,甲、乙两人必需不相邻的排法种数有:P
种。因此,甲、乙两人必需不相邻的排法种数有:P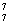 -2×P
-2×P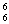 =3600,对照后应选B;
=3600,对照后应选B;
[解二]用插空法:P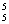 ×P
×P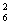 =3600。
=3600。
直接法是解答选择题最常用的基本方法,低档选择题可用此法迅速求解。直接法适用的范围很广,只要运算正确必能得出正确的答案。提高直接法解选择题的能力,准确地把握中档题目的“个性”,用简便方法巧解选择题,是建在扎实掌握“三基”的基础上,否则一味求快则会快中出错。
一些计算过程复杂的代数、三角、解析几何问题,可以作出有关函数的图像或者构造适当的几何图形,利用图示辅助进行直观分析,从而得出结论。这也就是数形结合的解题方法。
   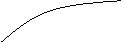   y y
 O 2 x
O 2 x |
[例5]不等式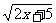 >x+1的解集是
。
>x+1的解集是
。
[解]如图,在同一坐标系中画出函数y=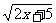 与y=x+1的图像,由图中可以直观地得到:-
与y=x+1的图像,由图中可以直观地得到:-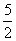 ≤x<2,所以所求解集是[-
≤x<2,所以所求解集是[-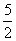 ,2)。
,2)。
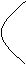 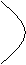    y
O 1 3|k| x y
O 1 3|k| x |
[例6](93年高考题)若双曲线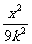 -
-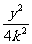 =1与圆x
=1与圆x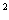 +y
+y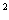 =1没有公共点,则实数k的取值范围是
。
=1没有公共点,则实数k的取值范围是
。
[解]在同一坐标系中作出双曲线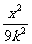 -
-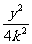 =1与圆x
=1与圆x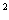 +y
+y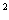 =1,由双曲线的顶点位置的坐标,可以得到|3k|>1,故求得实数k的取值范围是k>
=1,由双曲线的顶点位置的坐标,可以得到|3k|>1,故求得实数k的取值范围是k>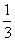 或k<-
或k<-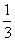 。
。
当填空题已知条件中含有某些不确定的量,但题目暗示答案可能是一个定值时,可以将变量取一些特殊数值、特殊位置、或者一种特殊情况来求出这个定值,这样,简化了推理、论证的过程。
[例3](89年高考题)已知(1-2x)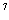 =a
=a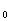 +a
+a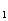 x+a
x+a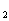 x
x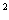 +…+a
+…+a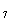 x
x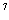 ,那么a
,那么a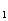 +a
+a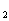 +…+a
+…+a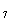 = 。
= 。
[解]令x=1,则有(-1)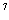 =a
=a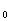 +a
+a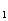 +a
+a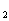 +…+a
+…+a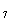 =-1;令x=0,则有a
=-1;令x=0,则有a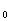 =1。所以a
=1。所以a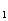 +a
+a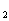 +…+a
+…+a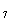 =-1-1=-2。
=-1-1=-2。
[例4](90年高考题)在三棱柱ABC-A’B’C’中,若E、F分别为AB、AC的中点,平面EB’C’F将三棱柱分成体积为V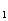 、V
、V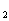 的两部分,那么V
的两部分,那么V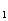 :V
:V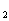 = 。
= 。
[解]由题意分析,结论与三棱柱的具体形状无关,因此,可取一个特殊的直三棱柱,其底面积为4,高为1,则体积V=4,而V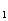 =
=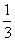 (1+
(1+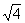 +4)=
+4)=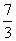 ,V
,V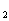 =V-V
=V-V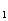 =
=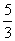 ,则V
,则V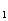 :V
:V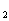 =7:5。
=7:5。
直接法就是根据数学概念,或者运用数学的定义、定理、法则、公式等,从已知条件出发,进行推理或者计算得出结果后,将所得结论填入空位处,它是解填空题最基本、最常用的方法。
[例1](94年高考题)已知sinθ+cosθ=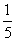 ,θ∈(0,π),则ctgθ的值是 。
,θ∈(0,π),则ctgθ的值是 。
[解]已知等式两边平方得sinθcosθ=-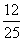 ,解方程组得sinθ=
,解方程组得sinθ=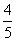 ,cosθ=
,cosθ=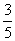 ,故答案为:-
,故答案为:-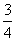 。
。
[另解]设tg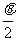 =t,再利用万能公式求解。
=t,再利用万能公式求解。
[例2](95年高考题)方程log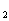 (x+1)
(x+1)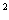 +log
+log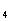 (x+1)=5的解是 。
(x+1)=5的解是 。
[解]由换底公式得4log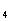 (x+1)+log
(x+1)+log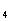 (x+1)=5,即log
(x+1)=5,即log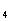 (x+1)=1,解得x=3。
(x+1)=1,解得x=3。
14. 若方程lg(kx)=2lg(x+1)只有一个实数解,求常数k的取值范围。
13. 已知z∈C,且|z|=1,求|(z+1)(z-i)|的最大值。
12. 已知函数y=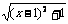 +
+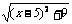 ,求函数的最小值及此时x的值。
,求函数的最小值及此时x的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com