
5.(2007陕西文)Rt△ABC的三个顶点在半径为13的球面上,两直角边的长分别为6和8,
则球心到平面ABC的距离是( )
 (A)5 (B)6 (C)10 (D)12
(A)5 (B)6 (C)10 (D)12
4.(2008湖北文、理)用与球心距离为1的平面去截球,
所得的截面面积为π,则球的休积为( )
A.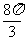 B.
B. 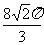 C.
C. D.
D. 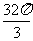
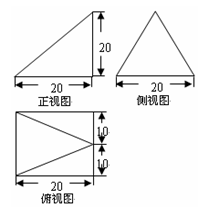
3.(2008山东文、理)右图是一个几何体的三视图 , 根据图中数据可得该几何体的表面积是( )
 (A)9π (B)10π (C)11π (D) 12π
(A)9π (B)10π (C)11π (D) 12π
2.(2004春招北京文、理)一个圆锥的侧面积是其底面积的2倍,则该圆锥的母线与底面所成的角为( )
A. 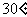 B.
B.
 C.
C.  D.
D.
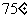
1.(2008全国Ⅱ卷文)正四棱锥的侧棱长为 ,侧棱与底面所成的角为
,侧棱与底面所成的角为 ,则该棱锥的体积为( )
,则该棱锥的体积为( )
A.3 B.6 C.9 D.18
20.(2008山东理)甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为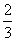 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为 且各人正确与否相互之间没有影响.用ε表示甲队的总得分.
(Ⅰ)求随机变量ε分布列和数学期望;
且各人正确与否相互之间没有影响.用ε表示甲队的总得分.
(Ⅰ)求随机变量ε分布列和数学期望;
(Ⅱ)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求P(AB).
19. (2007天津理) 已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率; (Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列和数学期望.
的分布列和数学期望.
18.(2007山东理)设 和
和 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量 表示方程
表示方程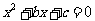 实根的个数(重根按一个计). (Ⅰ)求方程
实根的个数(重根按一个计). (Ⅰ)求方程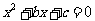 有实根的概率; (Ⅱ)求
有实根的概率; (Ⅱ)求 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)求在先后两次出现的点数中有5的条件下,方程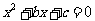 有实根的概率.
有实根的概率.
17. (2008广东理)随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获利分别为6万元、2万元、1万元,而1件次品亏损2万元,设1件产品的利润(单位:万元)为 .
.
(1)求ξ的分布列; (2)求1件产品的平均利润(即ξ的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%. 如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
16.(2008四川理) 设进入某商场的每一位顾客购买甲种商品的概率为 ,购买乙种商品的概率为
,购买乙种商品的概率为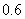 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)记 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求 的分布列及期望。
的分布列及期望。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com