
1.(2008湖南文).已知直线m,n和平面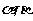 满足
满足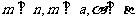 ,则( )
,则( )
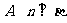
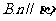 或
或
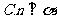 D
D 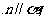 或
或
8.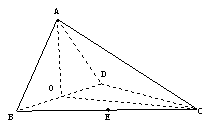 (2006福建文、理)如图,四面体ABCD中,O、E分别是BD、BC的中点,
(2006福建文、理)如图,四面体ABCD中,O、E分别是BD、BC的中点,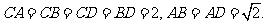
(I)求证: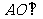 平面BCD; (II)求异面直线AB与CD所成角的大小;
平面BCD; (II)求异面直线AB与CD所成角的大小;
(III)求点E到平面ACD的距离。
7. (2006全国Ⅰ卷文、理)如图,
(2006全国Ⅰ卷文、理)如图,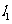 、
、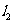 是互相垂直的异面直线,MN是它们的公垂线段.点A、B在
是互相垂直的异面直线,MN是它们的公垂线段.点A、B在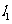 上,C在
上,C在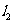 上,
上, 。 (Ⅰ)证明AC⊥NB;
。 (Ⅰ)证明AC⊥NB;
(Ⅱ)若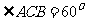 ,求
,求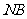 与平面ABC所成角的余弦值。
与平面ABC所成角的余弦值。
6.(2007四川理)如图,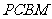 是直角梯形,∠
是直角梯形,∠ =90°,
=90°,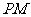 ∥
∥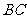 ,
,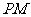 =1,
=1,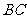 =2,又
=2,又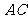 =1,∠
=1,∠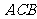 =120°,
=120°,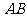 ⊥
⊥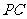 ,直线
,直线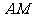 与直线
与直线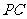 所成的角为60°.
所成的角为60°.
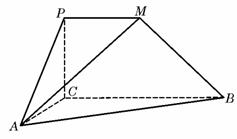 (Ⅰ)求证:平面
(Ⅰ)求证:平面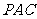 ⊥平面
⊥平面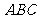 ; (Ⅱ)求二面角
; (Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求三棱锥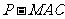 的体积.
的体积.
5. (2007海南、宁夏理)如图,在三棱锥
(2007海南、宁夏理)如图,在三棱锥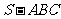 中,侧面
中,侧面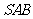 与侧面
与侧面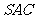 均为等边三角形,
均为等边三角形,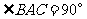 ,
, 为
为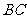 中点. (Ⅰ)证明:
中点. (Ⅰ)证明: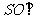 平面
平面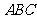 ;
;
(Ⅱ)求二面角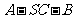 的余弦值.
的余弦值.
4.(2007安徽文、理)如图,在六面体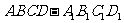 中,四边形ABCD是边长为2的正方形,四边形
中,四边形ABCD是边长为2的正方形,四边形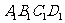 是边长为1的正方形,
是边长为1的正方形,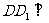 平面
平面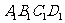 ,
,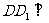 平面ABCD,DD1=2。
平面ABCD,DD1=2。
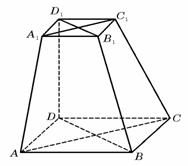 (Ⅰ)求证:
(Ⅰ)求证: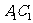 与AC共面,
与AC共面, 与BD共面.
与BD共面.
(Ⅱ)求证:平面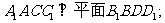
(Ⅲ)求二面角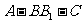 的大小.
的大小.
3.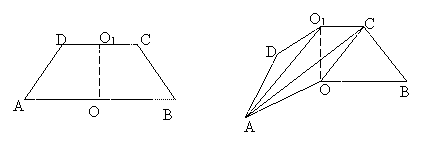 (2005湖南文、理)如图1,已知ABCD是上、下底边长分别为2和6,高为
(2005湖南文、理)如图1,已知ABCD是上、下底边长分别为2和6,高为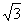 的等腰梯形,将它沿对称轴OO1折成直二面角,如图2。
的等腰梯形,将它沿对称轴OO1折成直二面角,如图2。
(Ⅰ)证明:AC⊥BO1; (Ⅱ)求二面角O-AC-O1的大小。
2.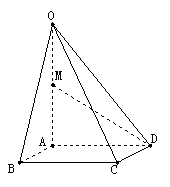 (2008安徽文)如图,在四棱锥
(2008安徽文)如图,在四棱锥 中,底面
中,底面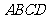 四边长为1的 菱形,
四边长为1的 菱形,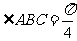 ,
,  ,
, 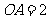 ,
,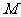 为
为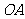 的中点。
的中点。
(Ⅰ)求异面直线AB与MD所成角的大小 ;
;
(Ⅱ)求点B到平面OCD的距离。
1.(2008海南、宁夏理)如图,已知点P在正方体ABCD-A1B1C1D1的对角线BD1上,∠PDA=60°。
 (1)求DP与CC1所成角的大小;(2)求DP与平面AA1D1D所成角的大小。
(1)求DP与CC1所成角的大小;(2)求DP与平面AA1D1D所成角的大小。
22.解:(Ⅰ)直角梯形ABCD的面积是
M底面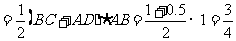 ,
,
∴ 四棱锥S-ABCD的体积是

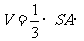 M底面
M底面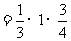
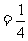 .
.
(Ⅱ)延长BA、CD相交于点E,连结SE,则SE是所求二面角的棱.
∵ AD∥BC,BC = 2AD,
∴ EA = AB = SA,∴ SE⊥SB,
∵ SA⊥面ABCD,得面SEB⊥面EBC,EB是交线,
又BC⊥EB,∴ BC⊥面SEB,故SB是CS在面SEB上的射影,∴ CS⊥SE,
所以∠BSC是所求二面角的平面角.
∵ 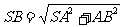
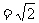 ,BC =1,BC⊥SB,
,BC =1,BC⊥SB,
∴ tg∠BSC 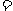
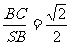 .
.
即所求二面角的正切值为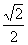 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com