
2. (2008重庆文)已知{an}为等差数列,a2+a8=12,则a5等于( )
(A)4 (B)5 (C)6 (D)7
1.(2007安徽文)等差数列 的前
的前 项和为
项和为 ,若
,若 ( )
( )
(A)12 (B)10 (C)8 (D)6
20.(2004天津理) 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F。 (1)证明PA//平面EDB;
 (2)证明PB⊥平面EFD; (3)求二面角C-PB-D的大小。
(2)证明PB⊥平面EFD; (3)求二面角C-PB-D的大小。
19.(2008天津文、理)如图,在四棱锥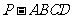 中,底面
中,底面 是矩形.已知
是矩形.已知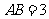 ,
, ,
, ,
,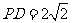 ,
,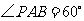 .
.
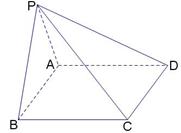 (Ⅰ)证明
(Ⅰ)证明 平面
平面 ;
;
(Ⅱ)求异面直线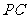 与
与 所成的角的大小;
所成的角的大小;
(Ⅲ)求二面角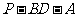 的大小.
的大小.
18.(2005辽宁)已知三棱锥P-ABC中,E、F分别是AC、AB的中点,△ABC,△PEF都是正三角形,PF⊥AB. (Ⅰ)证明PC⊥平面PAB; (Ⅱ)求二面角P-AB-C的平面角的余弦值;
 (Ⅲ)
若点P、A、B、C在一个表面积为12π的球面上,求△ABC的边长.
(Ⅲ)
若点P、A、B、C在一个表面积为12π的球面上,求△ABC的边长.
17.(2007天津文)如图,在四棱锥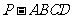 中,
中, 底面
底面 ,
,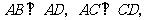

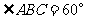 ,
,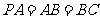 ,
,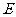 是
是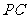 的中点.
的中点.
(Ⅰ)求 和平面
和平面 所成的角的大小;
所成的角的大小;
(Ⅱ)证明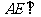 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
16.(2002春招北京文)在三棱锥S–ABC中,ÐSAB=ÐSAC=ÐACB=90°,AC=2,
 BC=
BC=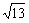 ,SB=
,SB=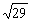 . (Ⅰ)证明:SC^BC;
. (Ⅰ)证明:SC^BC;
(Ⅱ)求侧面SBC与底面ABC所成的二面角大小;
(Ⅲ)求三棱锥的体积VS–ABC.
15. (2004湖南文)如图,在底面 是菱形的四棱锥P-ABCD中,
(2004湖南文)如图,在底面 是菱形的四棱锥P-ABCD中,
∠ABC=600,PA=AC=a,PB=PD= ,点E是PD的中点.
,点E是PD的中点.
(I)证明PA⊥平面ABCD, PB∥平面EAC;
(II)求以AC为棱,EAC与DAC为面的二面角 的正切值.
的正切值.
14. (2002春招上海)下图表示一个正方体表面的一种展开图,
(2002春招上海)下图表示一个正方体表面的一种展开图,
图中的四条线段AB、CD、EF和GH在原正方体中
相互异面的有 对.
13.(2005辽宁)如图,正方体的棱长为1,C、D分别是两条棱的中点,
A、B、M是顶点,那么点M到截面ABCD的距离是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com