
5.在△ABC中,已知 =
= ,判定△ABC是什么三角形。
,判定△ABC是什么三角形。
※§8.3空间向量及其运算
4.在△ABC中,已知B=30°,b=50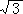 ,c=150,解三角形并判断三角形的形状。
,c=150,解三角形并判断三角形的形状。
3.某人在C点测得塔顶A在南偏西80°,仰角为45°,此人沿南偏东40°方向前进10米到0,测得塔顶A仰角为30°,则塔高= 。
2.△ABC中,若边a:b:c= :(1+
:(1+ ):2,则内角A=
。
):2,则内角A=
。
1.已知锐角三角形的边长分别为2,3,x,则第三边x的取值范围是( )
A.1<x<5 B. <x<
<x< C.
C. <x<5 D.1<x<
<x<5 D.1<x<
2.由于本节内容与代数、几何联系比较紧,故读者需对解斜三角形、解析几何中的圆锥曲线等知识非常熟悉方可。
三 经典例题导讲
[例1]在ABC中,已知a2=b2+bc+c2,则角A为( )
A. B.
B. C.
C. D.
D. 或
或
错解:选A
错因:公式记不牢,误将余弦定理中的“减”记作“加”。
正解:∵a2=b2+bc+c2=b2+c2-2bc(-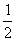 )=b2+c2-2bc·cos
)=b2+c2-2bc·cos
∴∠A=
选 C.
[例2]在△ABC中,已知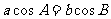 ,试判别其形状。
,试判别其形状。
错解:等腰三角形。
错因:忽视了两角互补,正弦值也相等的情形。直接由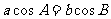 得,
得,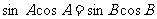 ,即
,即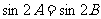 ,则
,则 。接着下结论,所求三角形为等腰三角形
。接着下结论,所求三角形为等腰三角形
正解:由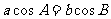 得,
得,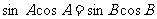 ,即
,即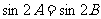
则 或
或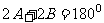 ,故三角形为直角三角形或等腰三角形。
,故三角形为直角三角形或等腰三角形。
[例3]过抛物线:y2=2px(p>0)顶点O作两条互相垂直的弦OA、OB(如图),求证:直线AB过一定点,并求出这一定点.
分析: 对于向量a=(x1,y1),b=(x2,y2),有a//b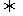 x1y2-x2y1=0.可以用来处理解析几何中的三点共线与两直线平行问题.
x1y2-x2y1=0.可以用来处理解析几何中的三点共线与两直线平行问题.
 证明:由题意知可设A点坐标为(
证明:由题意知可设A点坐标为( ,t1),B点坐标为(
,t1),B点坐标为( ,t2)
,t2)
∴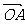 =(
=( ,t1),
,t1), 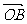 =(
=( ,t2),
,t2),
∵OA⊥OB,∴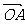 •
•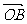 =0
=0
 •
• +t1•t2=0
+t1•t2=0
 t1•t2=-4p2 ①
t1•t2=-4p2 ①
设直线AB过点M(a,b),则 =(a-
=(a- ,b-t2),
,b-t2), =(
=( -
- ,t1-t2),
,t1-t2),
由于向量 与
与 是共线向量,∴(a-
是共线向量,∴(a- )(t1-t2)=
(b-t2)(
)(t1-t2)=
(b-t2)( -
- )
)
化简得2p(a-2p)=b(t1+t2)
显然当a=2p,b=0时等式对任意的成立
∴直线AB过定点,且定点坐标为M(2p,0)
四 典型习题导练
1.初中学过的勾股定理只是余弦定理的一种特殊情况。如当 =
= 时,
时,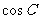 =0,此时有
=0,此时有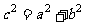 ;
;
2.正弦定理 在一个三角形中,各边和它所对角的正弦的比相等,并且都等于外接圆的直径,即

1.余弦定理:三角形任何一边的平方等于其他两边平方的和,减去这两边与它们夹角的余弦的积的2倍,即
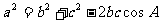
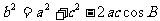

[例1] 和 = (3,-4)平行的单位向量是_________;
= (3,-4)平行的单位向量是_________;

错解:因为 的模等于5,所以与
的模等于5,所以与 平行的单位向量就是
平行的单位向量就是
 ,即 (,-)
,即 (,-)

错因:在求解平行向量时没有考虑到方向相反的情况。

正解:因为 的模等于5,所以与
的模等于5,所以与 平行的单位向量是
平行的单位向量是

 ,即(,-)或(-,)
,即(,-)或(-,)

点评:平行的情况有方向相同和方向相反两种。读者可以自己再求解“和 = (3,-4)垂直的单位向量”,结果也应该是两个。
= (3,-4)垂直的单位向量”,结果也应该是两个。

[例2]已知A(2,1),B(3,2),C(-1,4),若A、B、C是平行四边形的三个顶点,求第四个顶点D的坐标。

错解:设D的坐标为(x,y),则有x-2=-1-3,y-1=4-2 ,即x=-2,y=3。故所求D的坐标为(-2,3)。

错因:思维定势。习惯上,我们认为平行四边形的四个顶点是按照ABCD的顺序。其实,在这个题目中,根本就没有指出四边形ABCD。因此,还需要分类讨论。

正解:设D的坐标为(x,y)

当四边形为平行四边形ABCD时,有x-2=-1-3,y-1= 4-2 ,即x=
-2,y= 3。解得D的坐标为(-2,3);

当四边形为平行四边形ADBC时,有x-2=3-(-1),y-1= 2-4 ,即x= 6,y= -1。解得D的坐标为(6,-1);

当四边形为平行四边形ABDC时,有x-3=-1-2,y-2= 4-1 ,即x=
0,y= 5。解得D的坐标为(0,5)。

故第四个顶点D的坐标为(-2,3)或(6,-1)或(0,5)。

[例3]已知P1(3,2),P2(8,3),若点P在直线P1P2上,且满足|P1P|=2|PP2|,求点P的坐标。

错解:由|P1P|=2|PP2|得,点P 分P1P2所成的比为2,代入定比分点坐标公式得P( )
)

错因:对于|P1P|=2|PP2|这个等式,它所包含的不仅是点P为 P1,P2
的内分点这一种情况,还有点P是 P1,P2的外分点。故须分情况讨论。

正解:当点P为 P1,P2
的内分点时,P 分P1P2所成的比为2,此时解得P( );
);

当点P为 P1,P2
的外分点时,P 分P1P2所成的比为-2,此时解得P(13,4)。

则所求点P的坐标为( )或(13,4)。
)或(13,4)。

点评:在运用定比分点坐标公式时,要审清题意,注意内外分点的情况。也就是分类讨论的数学思想。

[例4] 设向量 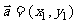 ,
, ,
, ,则“
,则“ ”是“
”是“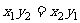 ”的
”的

A.充分不必要条件
B.必要不充分条件

C.充要条件
D.既不充分也不必要条件

分析:根据向量的坐标运算和充要条件的意义进行演算即可.

解:若 ,∵
,∵ ,则
,则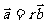 ,代入坐标得:
,代入坐标得: ,即
,即 且
且 .消去
.消去 ,得
,得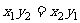 ;
;

反之,若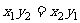 ,则
,则 且
且 ,即
,即


则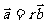 ,∴
,∴


故“ ”是“
”是“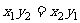 ”的充要条件.
”的充要条件.

答案:C

点评:本题意在巩固向量平行的坐标表示.

[例5].已知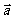 =(1,-1),
=(1,-1), =(-1,3),
=(-1,3), =(3,5),求实数x、y,使
=(3,5),求实数x、y,使 =x
=x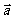 +y
+y .
.

分析:根据向量坐标运算和待定系数法,用方程思想求解即可.

解:由题意有

x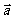 +y
+y =x(1,-1)+y(-1,3)=(x-y,-x+3y).
=x(1,-1)+y(-1,3)=(x-y,-x+3y).

又 =(3,5)
=(3,5)

∴x-y=3且-x+3y=5

解之得 x=7 且y=4

点评:在向量的坐标运算中经常要用到解方程的方法.

[例6]已知A(-1,2),B(2,8), =
=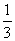
 ,
,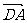 = -
= -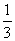
 ,求点C、D和向量
,求点C、D和向量 的坐标.
的坐标.

分析:待定系数法设定点C、D的坐标,再根据向量
 ,
,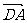 和
和 关系进行坐标运算,用方程思想解之.
关系进行坐标运算,用方程思想解之.

解:设C、D的坐标为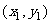 、
、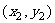 ,由题意得
,由题意得

 =(
=(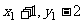 ),
), =(3,6),
=(3,6), 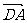 =(
=(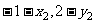 ),
), =(-3,-6)
=(-3,-6)

又 =
=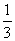
 ,
,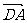 = -
= -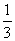



∴(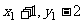 )=
)=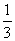 (3,6), (
(3,6), (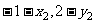 )=-
)=-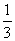 (-3,-6)
(-3,-6)
即 (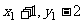 )=(1,2) , (
)=(1,2) , (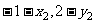 )=(1,2)
)=(1,2)
∴ 且
且 ,
, 且
且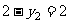
∴ 且
且 ,且
,且
∴点C、D和向量 的坐标分别为(0,4)、(-2,0)和(-2,-4)
的坐标分别为(0,4)、(-2,0)和(-2,-4)
小结:本题涉及到方程思想,对学生运算能力要求较高.
§8.2平面向量与代数、几何的综合应用
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com