5. - Shall we go on a picnic?　　 -That’s going to be ______

A.　　　 fun 　B. funny 　C. fun 　D. very fun

4. Jim and Bill don’t live _____ the middle school.

A. away from 　B. far from　 C. far away 　D. far

3. They have decided to go to work _____every day.

A. by bikes 　B. on feet　 C. by bus 　D. in car

2. Jack began to do his homework as soon as he____ home.

A. came to 　B. reached　 C. arrived at 　D. got to

1. The bus station is about five hundred meters____ here，it’s within walking distance.

A. away from 　B. away　 C. far away from 　D. far from

12.设函数f(x)在(-∞,+∞)上满足f(2-x)=f(2+x)，f(7-x)=f(7+x)，且在闭区间［0，7］上，只有f(1)=f(3)=0.

(1)试判断函数y=f(x)的奇偶性；　

(2)试求方程f(x)=0在闭区间［-2 005，2 005］上的根的个数，并证明你的结论.

解 (1)由

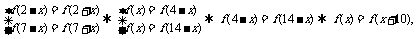　从而知函数y=f(x)的周期为T=10.又f(3)=f(1)=0,而f(7)≠0,故f(-3)≠0.　

故函数y=f(x)是非奇非偶函数.　

(2)由(1)知y=f(x)的周期为10.　

又f(3)=f(1)=0,f(11)=f(13)=f(-7)=f(-9)=0,　

故f(x)在［0，10］和［-10，0］上均有两个解，从而可知函数y=f(x)在［0，2 005］上有402个解，在［-2 005，0］上有400个解，所以函数y=f(x)在［-2 005，2 005］上有802个解.

11.已知函数f(x)=x²+|x-a|+1,a∈R.　

(1)试判断f(x)的奇偶性；　

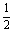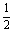(2)若-≤a≤，求f(x)的最小值.

解 　(1)当a=0时，函数f(-x)=(-x)²+|-x|+1=f(x),　

此时,f(x)为偶函数.当a≠0时，f(a)=a²+1,f(-a)=a²+2|a|+1,　

f(a)≠f(-a),f(a)≠-f(-a),此时，f(x) 为非奇非偶函数.　

(2)当x≤a时,f(x)=x²-x+a+1=(x-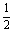)²+a+,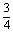　

∵a≤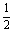,故函数f(x)在(-∞，a］上单调递减，　

从而函数f(x)在(-∞，a］上的最小值为f(a)=a²+1.　

当x≥a时，函数f(x)=x²+x-a+1=(x+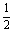)²-a+,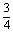　

∵a≥-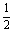，故函数f(x)在［a，+∞)上单调递增，从而函数f(x)在［a，+∞)上的最小值为f(a)=a²+1.　

综上得，当-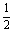≤a≤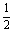时，函数f(x)的最小值为a²+1.　

10.已知f(x)是R上的奇函数，且当x∈(-∞,0)时，f(x)=-xlg(2-x),求f(x)的解析式.　

解　 ∵f(x)是奇函数，可得f(0)=-f(0),∴f(0)=0.　

当x＞0时，-x＜0,由已知f(-x)=xlg(2+x),∴-f(x)=xlg(2+x)，　

即f(x)=-xlg(2+x) (x＞0).∴f(x)=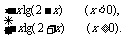

即f(x)=-xlg(2+|x|) (x∈R).

9.已知f(x)是实数集R上的函数，且对任意x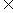R,f(x)=f(x+1)+f(x-1)恒成立.

　 (1)求证：f(x)是周期函数.

　 (2)已知f(3)=2，求f(2 004).

　 　(1)证明　 ∵f(x)=f(x+1)+f(x-1),∴f(x+1)=f(x)-f(x-1),

则f(x+2)=f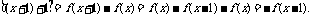

∴f(x+3)=f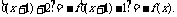

∴f(x+6)=f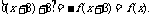

∴f(x)是周期函数且6是它的一个周期.

(2)解 　f(2 004)=f(334×6)=f(0)=-f(3)=-2.

8.f(x)、g(x)都是定义在R上的奇函数，且F(x)=3f(x)+5g(x)+2,若F(a)=b,则F(-a)=　　　　 .　

答案　 -b+4