
3.登山运动员在登雪山时要注意防止紫外线的过度照射,尤其是眼睛更不能长时间被紫外线照射,否则将会严重地损伤视力.有人想利用薄膜干涉的原理设计一种能大大减小紫外线对眼睛伤害的眼镜.他选用的薄膜材料的折射率为n=1.5,所要消除的紫外线的频率为ν=8.1×1014 Hz.
(1)他设计的这种“增反膜”所依据的原理是______________________________.
(2)这种“增反膜”的厚度至少是多少?
(3)以下有关薄膜干涉的说法正确的是 ( )
A.薄膜干涉说明光具有波动性
B.如果薄膜的厚度不同,产生的干涉条纹一定不平行
C.干涉条纹一定是彩色的
D.利用薄膜干涉也可以“增透”
解析:(1)为了减少进入眼睛的紫外线,应使入射光分别从该膜的前后两个表面反射后形成的反射光叠加后加强,从而使透射的紫外线减弱.
(2)路程差(大小等于薄膜厚度d的2倍)应等于光在薄膜中的波长λ′的整数倍,即2d=Nλ′(N=1,2…),因此,膜的厚度至少是紫外线在膜中波长的,紫外线在真空中的波长是λ=c/ν≈3.7×10-7 m.在膜中的波长是λ′=λ/n≈2.47×10-7 m,故膜的厚度至少是1.23×10-7 m.
(3)干涉和衍射都证明光具有波动性;如果薄膜厚度均匀变化,则干涉条纹一定平行;白光的干涉为彩色条纹,单色光的干涉则为该色光颜色;当膜的厚度为四分之一波长时,两反射光叠加后减弱则会“增透”.故选项A、D正确.
 答案:(1)两反射光叠加后加强
答案:(1)两反射光叠加后加强
(2)1.23×10-7 m (3)AD
2.两个狭缝相距0.3 mm,位于离屏50 cm处,现用波长为6000 的光照射双缝,求:
(1)两条相邻暗条纹间的距离是多少?
(2)若将整个装置放于水中,那么两条相邻暗条纹间的距离是多少?(水的折射率
为,1 =10-10 m)
解析:本题要求用公式Δx=λ进行计算.
(1)Δx=λ= m
=1×10-3 m=1 mm
(2)λ′== =4500
Δx′=λ′= m=0.75 mm.
答案:(1)1 mm (2)0.75 mm
1.用某一单色光做双缝干涉实验时,已知双缝间距离为0.25 mm,在距离双缝为1.2 m处的光屏上,测得5条亮纹间的距离为7.5 mm,试求所用单色光的波长.
解析:已知Δx==×10-3 m,l=1.20 m,
d=0.25×10-3 m,根据公式Δx=λ得
波长λ=Δx= m
≈3.906×10-7 m.
答案:3.906×10-7 m
1.5,求:
(1)这束入射光线的入射角多大?
(2)光在棱镜中的波长是多大?
(3)该束光线第一次从CD面出射时的折射角.(结果可用三角函数表示)
解析:(1)设光在AD面的入射角、折射角分别为θ1、θ2,θ2=30°
根据n=得sinθ1=nsinθ2=1.5×sin30°=0.75,
θ1=arcsin0.75.
(2)根据n=得
v== m/s=2×108 m/s,
根据v=λf得
λ== m≈3.77×10-7 m.
(3)光路如图所示,光线ab在AB面的入射角为45°,
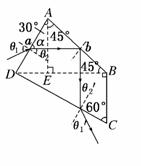
设玻璃的临界角为C,则
sinC==≈0.67
sin45°>0.67,因此光线ab在AB面会发生全反射
光线在CD面的入射角θ2′=θ2=30°
根据n=,光线在CD面的出射光线与法线的夹角θ1′=θ1=arcsin0.75.
答案:(1)arcsin0.75 (2)3.77×10-7 m (3)arcsin0.75
5.3×1014 Hz的单色细光束从AD面入射,在棱镜中的折射光线如图中ab所示,ab
与AD面的夹角α=60°.已知光在真空中的速度c=3×108 m/s,玻璃的折射率n=
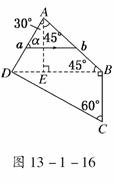
9.(2010·南通模拟)如图13-1-16所示,玻璃棱镜ABCD可以看
成是由ADE、ABE、BCD三个直角三棱镜组成.一束频率为
8.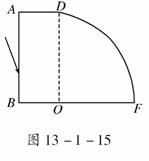 如图13-1-15所示为用某种透明材料制成的一块柱体形棱镜的水平截面图,FD为圆周,圆心为O,光线从AB面入射,入射角θ1=60°,它射入棱镜后射在BF面上的O点并恰好不从BF面射出.
如图13-1-15所示为用某种透明材料制成的一块柱体形棱镜的水平截面图,FD为圆周,圆心为O,光线从AB面入射,入射角θ1=60°,它射入棱镜后射在BF面上的O点并恰好不从BF面射出.
(1)画出光路图;
(2)求该棱镜的折射率n和光线在棱镜中传播的速度大小v(光在
真空中的传播速度c=3.0×108 m/s).
解析:(1)光路图如图所示.
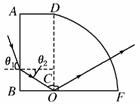 (2)设光线在AB面的折射角为θ2,折射光线与OD的夹角为C,
(2)设光线在AB面的折射角为θ2,折射光线与OD的夹角为C,
则n=.
由题意,光线在BF面恰好发生全反射,sinC=,由图可知,
θ2+C=90°
联立以上各式解出n≈1.3(或)
又n=,故解出v≈2.3×108 m/s(或×108 m/s).
答案:(1)见解析图
 (2)1.3(或) 2.3×108 m/s(或×108 m/s)
(2)1.3(或) 2.3×108 m/s(或×108 m/s)
7.(2010·苏南模拟)一台激光器,它的功率为P,如果它发射出的单色光在空气中的波长
为λ.
(1)它在时间t内辐射的光能为__________,如果已知这束单色光在某介质中的传播速度为v,那么这束单色光从该介质射向真空发生全反射的临界角为__________.
 (2)由于激光是亮度高、平行度好、单色性好的相干光,所以光导纤维中用激光作为信息高速传输的载体.要使射到粗细均匀的圆形光导纤维一个端面上的激光束都能从另一个端面射出,而不会从侧壁“泄漏”出来,光导纤维所用材料的折射率至少应为多大?
(2)由于激光是亮度高、平行度好、单色性好的相干光,所以光导纤维中用激光作为信息高速传输的载体.要使射到粗细均匀的圆形光导纤维一个端面上的激光束都能从另一个端面射出,而不会从侧壁“泄漏”出来,光导纤维所用材料的折射率至少应为多大?
解析:(1)激光器t时间内发出的光能W=Pt
由n=,sinC=,则C=arcsin.
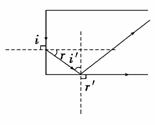
(2)设激光束在光导纤维端面的入射角为i,折射角为r,折射光线射向侧面时的入射角为i′,折射角为r′,如图所示.
由折射定律:n=,
由几何关系:r+i′=90°,sinr=cosi′.
由全反射临界角的公式:
sini′=,
cosi′= ,
要保证从端面射入的任何光线都能发生全反射,应有i=r′=90°,sini=1.故
n===,
解得n=,故光导纤维的折射率至少应为.
答案:(1)Pt arcsin (2)
6.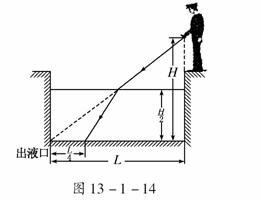 如图13-1-14所示,巡查员站立于一空的贮液池边,检查池角出液口的安全情况.已知池宽为L,照明灯到池底的距离为H,若保持照明光束方向不变,向贮液池中注入某种液体,当液面高为时,池底的光斑距离出液口.
如图13-1-14所示,巡查员站立于一空的贮液池边,检查池角出液口的安全情况.已知池宽为L,照明灯到池底的距离为H,若保持照明光束方向不变,向贮液池中注入某种液体,当液面高为时,池底的光斑距离出液口.
(1)试求:当液面高为H时,池底的光斑到出液口的距离x.
(2)控制出液口缓慢地排出液体,使液面以vh的速率匀速下降,试求池底的光斑移动的速率vx.
解析:(1)作出光路图如图所示.
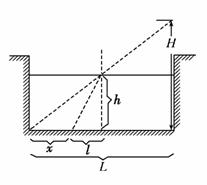 由几何关系知:
由几何关系知:
= ①
由折射定律:
=n· ②
代入h=、l=得:
n= ③
联立①②③式得x=·h.
当h=H时,解得x=.
(2)由x=·h知,Δx=·Δh,则
=·,即vx=·vh.
答案:(1) (2)·vh
5.(2009·海南高考)如图13-1-13所示,一透明半圆柱体折射率为n=2,半径为R,长为L.一平行光束从半圆柱体的矩形表面垂直射入,从部分柱面有光线射出.求该部分柱面的面积S.
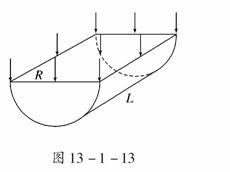
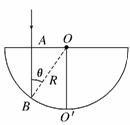
解析:半圆柱体的横截面如图所示,OO′为半径.设从A点入射的光线在B点处恰好满足全反射条件,由折射定律有
sinθ=
式中,θ为全反射临界角.由几何关系得
∠O′OB=θ
S=2RL·∠O′OB
代入题所给条件得
S=RL.
答案:RL
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com