1.下面函数图像描述的是某商品在半年中的价格走势，根据该图，下列理解正确的有　 (　)

①该商品很可能供不应求　　　　　　

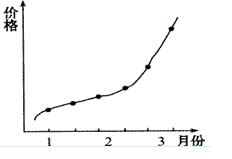
②该商品的互补商品需求量会有所增加

③生产者可能会扩大该商品生产　　　

④该商品的替代商品需求量会有所增加

A．①②④　　 B. ①②③　 C. ②③④　 　D. ①③④

12．(16分)如图所示，甲船由A岛出发向北偏东45°的方向作匀速直线航行，速度为15海里/小时，在甲船从A岛出发的同时，乙船从A岛正南40海里处的B岛出发，朝北偏东θ的方向作匀速直线航行，速度为10海里/小时．

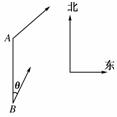
(1)求出发后3小时两船相距多少海里？

(2)求两船出发后多长时间距离最近？最近距离为多少海里？

(3)两船在航行中能否相遇？试说明理由．

[解析]　以A为原点，BA所在直线为y轴建立如图所示的平面直角坐标系．设在t时刻甲、乙两船分别在P(x₁，y₁)，Q(x₂，y₂)．

则.

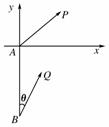
由tan θ＝可得，cos θ＝，sin θ＝，

故.

(1)令t＝3，P、Q两点的坐标分别为(45,45)，(30,20)，

|PQ|＝＝＝5.

即出发后3小时两船相距5海里．

(2)由(1)的解法过程易知：

|PQ|＝

＝

＝＝≥20，

∴当且仅当t＝4时，|PQ|取得最小值20.

即两船出发后4小时时距离最近，最近距离为20海里．

(3)射线AP的方程为y＝x(x≥0)，

射线BQ的方程为y＝2x－40(x≥0)．

它们的交点为M(40,40)，若甲、乙两船相遇，则应在M点处．

此时，|AM|＝＝40，

甲船到达M点所用的时间为：t_甲＝＝＝(小时)，

|BM|＝＝40，

乙船到达M点所用的时间为：t_乙＝＝4(小时)，

∵t_甲≠t_乙，∴甲、乙两船不会相遇．

11．(15分)(2009年山东卷)已知函数f(x)＝2sin xcos²+cos xsin φ－sin x(0＜φ＜π)在x＝π处取最小值．

(1)求φ的值；

(2)在△ABC中，a，b，c分别是角A，B，C的对边，已知a＝1，b＝，f(A)＝， 求角C.

[解析]　(1)f(x)＝2sin x+cos xsin φ－sin x

＝sin x+sin xcos φ+cos xsin φ－sin x

＝sin xcos φ+cos xsin φ＝sin(x+φ)．

因为f(x)在x＝π时取最小值，

所以sin(π+φ)＝－1，故sin φ＝1.

又0＜φ＜π，所以φ＝.

(2)由(1)知f(x)＝sin＝cos x.

因为f(A)＝cos A＝，

且A为△ABC的内角，所以A＝.

由正弦定理得sin B＝＝，

又b＞a，所以B＝或B＝.

当B＝时，C＝π－A－B＝π－－＝，

当B＝时，C＝π－A－B＝π－－＝.

综上所述，C＝或C＝.

10．(15分)已知△ABC的周长为+1，且sin A+sin B＝sin C.

(1)求边AB的长；

(2)若△ABC的面积为sin C．求角C的度数．

[解析]　(1)由题意及正弦定理，得AB+BC+AC＝+1.

BC+AC＝AB，两式相减，得AB＝1.

(2)由△ABC的面积＝BC·AC·sin C＝sin C，

得BC·AC＝.

由余弦定理，得cos C＝

＝＝，

∴C＝60°.

9．在△ABC中，A、B、C所对的边分别为a、b、c，且满足a+b+c＝+1，sin A+sin B＝sin C，则c＝________；若C＝，则△ABC的面积S＝________.

[解析]　依题意及正弦定理得a+b＝c，且a+b+c＝+1，因此c+c＝+1，c＝1，当C＝时，

c²＝a²+b²－2abcos C＝a²+b²－ab＝1，∴(a+b)²－3ab＝1.

又a+b＝，因此2－3ab＝1，

∴ab＝，则△ABC的面积S＝absin C＝×sin＝.

[答案]　1　

8．在△ABC中，AB＝2，AC＝，BC＝1+，AD为边BC上的高，则AD的长是________．

[解析]　如图由余弦定得：cos B＝＝⇒B＝，故AD＝ABsin ＝2×＝.

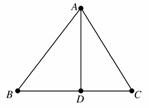
[答案]　

7．在△ABC中，设命题p：＝＝；命题q：△ABC是等边三角形．那么命题p是命题q的________条件．

[解析]　命题p：＝＝.

由正弦定理＝＝，

∴sin A＝sin B＝sin C，

∴A＝B＝C⇒a＝b＝c.反之，过程亦成立．

[答案]　充分必要

6．一船自西向东航行，上午10时到达灯塔P的南偏西75°、距塔68海里的M处，下午2时到达这座灯塔的东南方向的N处，则这只船航行的速度为

(　)

A.海里/时　 　　　　　　　　　　　 B．34海里/时

C.海里/时　 　　　　　　　　　　　 D．34海里/时

[解析]　如图，由题意知∠MPN＝75°+45°＝120°，

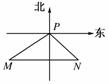
∠PNM＝45°.

在△PMN中，由正弦定理，得

＝，

∴MN＝68×＝34.

又由M到N所用时间为14－10＝4(小时)，

∴船的航行速度v＝

＝(海里/时)．

[答案]　A

5．在△ABC中，角A、B、C所对的边分别为a，b，c，若b²+c²－bc＝a²，且＝，则角C的值为

(　)

A．45°　 　　　　　　　　　　　　　　 B．60°

C．90° 　　　　　　　　　　　　　　　 　D．120°

[解析]　由b²+c²－bc＝a²得b²+c²－a²＝bc，

∴cos A＝＝，∴A＝60°.

又＝，∴＝，

∴sin B＝sin A＝×＝，

∴B＝30°，∴C＝180°－A－B＝90°.

[答案]　C

4．满足A＝45°，c＝，a＝2的△ABC的个数记为m，则a^m的值为

(　)

A．4　 　　　　　　　　　　　　　　　 B．2

C．1　 　　　　　　　　　　　　　　　 D．不确定

[解析]　由正弦定理＝

得sin C＝＝＝.

∵c＞a，∴C＞A＝45°，

∴C＝60°或120°，

∴满足条件的三角形有2个，

即m＝2.∴a^m＝4.

[答案]　A