
8.设方程x2–2x+m=0的两个根为a、b,且|a–b|=2,则实数m的值是 .
7.某项工程由下列工序组成:则工程总时数为 _.
|
工序 |
a |
b |
c |
d |
e |
f |
|
紧前工序 |
-- |
-- |
a、b |
c |
c |
d、e |
|
工时(天) |
2 |
4 |
5 |
7 |
4 |
3 |
6.方程2cos2x = 1的解是 .
5.现有形状特征一样的若干个小球,每个小球上写着一个两位数,一个口袋里放有标着所有不同的两位数的小球,现任意取一个小球,取出小球上两位数的十位数字比个位数字大的概率是 .
4.向量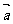 、
、 满足|
满足|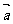 |=2,|
|=2,| |=3,且|
|=3,且|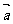 +
+ |=
|=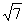 ,则
,则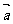 .
. = .
= .
3.等差数列{an}中,a5+a8+ a11+ a14+ a17=50,则S21= .
2.已知f(x)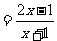 ,则
,则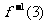 =____________.
=____________.
1.设全集U ={a、b、c、d、e}, 集合A={a、b},B={b、c、d},则A∩CUB=________.
1 函数y=
函数y=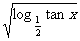 的定义域是( )
的定义域是( )
A {x|0<x≤
{x|0<x≤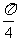 )
B
)
B {x|2kπ<x≤2kπ+
{x|2kπ<x≤2kπ+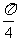 ,k∈Z
,k∈Z
C {x|kπ<x≤kπ+
{x|kπ<x≤kπ+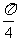 ,k∈Z
,k∈Z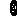 D
D {x|kπ-
{x|kπ- <x≤kπ+
<x≤kπ+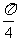 ,k∈Z
,k∈Z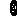
解析:由log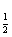 tanx≥0,得0<tanx≤1
tanx≥0,得0<tanx≤1
根据y=tanx在x∈(- ,
, )上的图象可知0<x≤
)上的图象可知0<x≤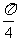
结合周期性,可知原函数的定义域为:{x|kπ<x≤kπ+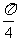 ,k∈Z}
,k∈Z}
答案:C
2 求函数y=
求函数y=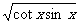 的定义域
的定义域
解:∵cotxsinx=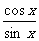 ·sinx=cosx
·sinx=cosx
∴函数的定义域由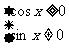 确定
确定
解之得2kπ- ≤x≤2kπ+
≤x≤2kπ+ ,且x≠kπ,(k∈Z)
,且x≠kπ,(k∈Z)
从而原函数的定义域为:[2kπ- ,2kπ
,2kπ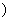 ∪(2kπ,2kπ+
∪(2kπ,2kπ+
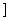 (k∈Z)
(k∈Z)
3 如果α、β∈(
如果α、β∈( ,π)且tanα<cotβ,那么必有( )
,π)且tanα<cotβ,那么必有( )
A α<β
B
α<β
B β<α
β<α
C α+β<
α+β<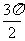 D
D α+β>
α+β>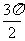
解:tanα<cotβ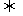 tanα<tan(
tanα<tan(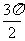 -β
-β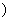
∵α、β∈( ,π),
,π),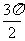 -β∈(
-β∈( ,π)
,π)
又∵y=tanx在( ,π)上是增函数
,π)上是增函数
∴α<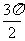 -β 即α+β<
-β 即α+β<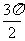
答案:C
4 函数y=lg(tanx)的增函数区间是( )
函数y=lg(tanx)的增函数区间是( )
A (kπ-
(kπ- ,kπ+
,kπ+ )(k∈Z) B
)(k∈Z) B (kπ,kπ+
(kπ,kπ+ )(k∈Z)
)(k∈Z)
C (2kπ-
(2kπ- ,2kπ+
,2kπ+ )(k∈Z) D
)(k∈Z) D (kπ,kπ+π)(k∈Z)
(kπ,kπ+π)(k∈Z)
解:函数y=lg(tanx)为复合函数,要求其增函数区间则要满足tanx>0,且y=tanx是增函数的区间
解之得kπ<x<kπ+ (k∈Z)
(k∈Z)
∴原函数的增函数区间为:(kπ,kπ+ )(k∈Z)
)(k∈Z)
答案:B
5 试讨论函数y=logatanx的单调性
试讨论函数y=logatanx的单调性
解:y=logatanx可视为y=logau与u=tanx复合而成的,复合的条件为tanx>0,
即x∈(kπ,kπ+ )(k∈Z)
)(k∈Z)
①当a>1时,y=logau在u∈(0,+∞)上单调递增;
当x∈(kπ,kπ+ )时,u=tanx是单调递增的,
)时,u=tanx是单调递增的,
∴y=logatanx在x∈(kπ,kπ+ )(k∈Z)上是单调增函数
)(k∈Z)上是单调增函数
②当0<a<1时,y=logau在u∈(0,+∞)上单调递减;
当x∈(kπ,kπ+ )时,u=tanx是单调递增的
)时,u=tanx是单调递增的
∴y=logatanx在x∈(kπ,kπ+ )(k∈Z)上是单调减函数
)(k∈Z)上是单调减函数
故当a>1时,y=logatanx在x∈(kπ,kπ+ )(k∈Z)上单调递增;
)(k∈Z)上单调递增;
当0<a<1时,y=logatanx在x∈(kπ,kπ+ )(k∈Z)上单调递减;
)(k∈Z)上单调递减;
3.求函数y=tan2x的定义域、值域和周期、并作出它在区间[-π,π]内的图象
解:(1)要使函数y=tan2x有意义,必须且只须2x≠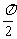 +kπ,k∈Z
+kπ,k∈Z
即x≠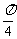 +
+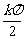 ,k∈Z
,k∈Z
∴函数y=tan2x的定义域为{x∈R|,x≠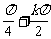 ,k∈Z}
,k∈Z}
 (2)设t=2x,由x≠
(2)设t=2x,由x≠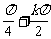 ,k∈Z}知t≠
,k∈Z}知t≠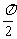 +kπ,k∈Z
+kπ,k∈Z
∴y=tant的值域为(-∞,+∞)
即y=tan2x的值域为(-∞,+∞)
(3)由tan2(x+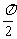 )=tan(2x+π)=tan2x
)=tan(2x+π)=tan2x
∴y=tan2x的周期为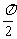 .
.
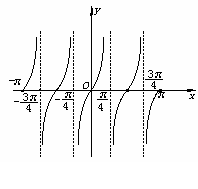
(4)函数y=tan2x在区间[-π,π]的图象如图
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com