
1.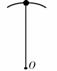 如图,一轻杆一端固定在O点,另一端固定一小球,在竖直平面内做圆周运动,通过最高点时,由于球对杆有作用,使杆发生了微小形变,关于杆的形变量与球在最高点时的速度大小关系,正确的是 (
C )
如图,一轻杆一端固定在O点,另一端固定一小球,在竖直平面内做圆周运动,通过最高点时,由于球对杆有作用,使杆发生了微小形变,关于杆的形变量与球在最高点时的速度大小关系,正确的是 (
C )
A.形变量越大,速度一定越大 B.形变量越大,速度一定越小
C.形变是为零,速度一定不为零 D.速度为零,可能无形变
3.圆周运动中的临界问题:
(1)没有别的物体支持的质点做圆周运动,如细绳系着的物体或沿圆环内壁运动的物体在竖直平面内做圆周运动,在通过轨道最高点时的速度的临界值为υ = .当υ≥时,物体能通过最高点;当υ<时,物体还没有到最高点时,就脱离了轨道.
(2)受别的物体约速的质点做圆周运动,如套在圆环上的物体,有轻杆或管约束的物体在竖直平面内做圆周运动,当通过最高点时,物体通过最高点的速度可以为任何值,即υ≥0.当υ>时,环、杆或管对物体的作用力方向向下;当υ= 时,没有作用力;当0<υ<时,作用力方向向上.
规律方法
 [例1]如图所示,质量为m的物块与转台之间能出现的最大静摩擦力为物块重力的k倍,它与转台转轴OO′相距R,物块随转台由静止开始转动,当转速增加到一定值时,物块即将在转台上滑动,在物块由静止到相对转台开始滑动前的这一过程中,转台对物块做的功为
( B )
[例1]如图所示,质量为m的物块与转台之间能出现的最大静摩擦力为物块重力的k倍,它与转台转轴OO′相距R,物块随转台由静止开始转动,当转速增加到一定值时,物块即将在转台上滑动,在物块由静止到相对转台开始滑动前的这一过程中,转台对物块做的功为
( B )
A.0 B.小于kmgR
C.等于kmgR D.大于kmgR
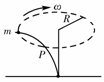 训练题 如图所示,质量不计的轻质弹性杆P插入桌面上的小孔中,杆的另一端固定有一个质量为m的小球.使小球在水平面内作半径为R的匀速圆周运动,且角速度为ω,则杆的上端受到球对杆的作用力大小为
( C
)
训练题 如图所示,质量不计的轻质弹性杆P插入桌面上的小孔中,杆的另一端固定有一个质量为m的小球.使小球在水平面内作半径为R的匀速圆周运动,且角速度为ω,则杆的上端受到球对杆的作用力大小为
( C
)
A.mω2R
B.m
C.m
D.不能确定
[例2]如图所示,线的上端固定,下端系一小球,将小球与线拉到一水平位置后从静止开始释放,求小球的摆线运动到与水平方向成多大角度时,球获得最大的竖直分速度?(反三角函数表示).
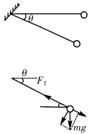 [解析]设小球从线水平开始转过角度θ时,速度为v,此过程中机械能守恒,则有:mglsinθ = mυ2,得:υ2 =
2glsinθ
[解析]设小球从线水平开始转过角度θ时,速度为v,此过程中机械能守恒,则有:mglsinθ = mυ2,得:υ2 =
2glsinθ
此时小球受重力mg和线的拉力FT,如图所示,在沿绳方向,由牛顿第二定律有:FT-mgsinθ = m,代入υ2得:FT = 3mgsinθ
小球在竖直方向先加速后减速,当小球在竖直方向的加速度为零时,可获得最大的竖直分速度,即:FTsinθ-mg = 0,代入Ft可得sin2θ =
 即当θ = arcsin()时,小球获得竖直方向最大的分速度.
即当θ = arcsin()时,小球获得竖直方向最大的分速度.
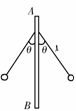
训练题如图所示,已知瓦特节速器上有固定有重球的两根棒,棒长各为20cm,电机在运动转时,两棒与竖直的转轴AB之间夹角为60°,如图所示,求此时节速器的转速为多少?
答案:n=96r/min
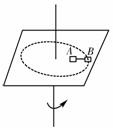 [例3]如图所示,水平转台上放有质量均为m的两小物块A、B,A离转轴距离为L,A、B间用长为L的细线相连,开始时A、B与轴心在同一直线上,线被拉直,A、B与水平转台间最大静摩擦力均为重力的μ倍,当转台的角速度达到多大时线上出现张力wh当转台的角速度达到多大时A物块开始滑动?
[例3]如图所示,水平转台上放有质量均为m的两小物块A、B,A离转轴距离为L,A、B间用长为L的细线相连,开始时A、B与轴心在同一直线上,线被拉直,A、B与水平转台间最大静摩擦力均为重力的μ倍,当转台的角速度达到多大时线上出现张力wh当转台的角速度达到多大时A物块开始滑动?
[解析]线上刚开始出现张力时,B受的最大静摩擦力刚好充当向心力,即:μmg = mω2(2L),得ω =
当A所受摩擦力达到最大静摩擦力时,A开始滑动,设此时线中张力为F,由牛顿第二定律,对A有:μmg-F = mω′2L
对B有:F+μmg = mω′2(2L)
由上述两式有:ω′ =
即当转台的角速度达到时,线上开始出现张力,当角速度达到时,A开始滑动.
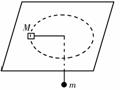 训练题如图所示,细绳一端系看质量M = 0.6kg的物体静止于水平面,另一端通过光滑小孔吊着质量m = 0.3kg的物体,M的中点与圆孔距离为0.2m,设M和水平面间的最大静摩擦力为2N,现使此平面绕中心轴线转动,问角速度ω在什么范围m会处于静止状态?(取g = 10m/s2)
训练题如图所示,细绳一端系看质量M = 0.6kg的物体静止于水平面,另一端通过光滑小孔吊着质量m = 0.3kg的物体,M的中点与圆孔距离为0.2m,设M和水平面间的最大静摩擦力为2N,现使此平面绕中心轴线转动,问角速度ω在什么范围m会处于静止状态?(取g = 10m/s2)
答案:2。9r/s≤ω≤6。5r/s
能力训练
2.圆周运动中的向心力:
向心力可以是重力、弹力、摩擦力等各种力,也可以是各力的合力或某力的分力?向心力是按力的作用效果来命名的,故在分析做圆周运动的物体受力时,切不可在性质力上再添加一个向心力,但对各种情况下向心力的来源应明确.
圆周运动中的动力学方程即将牛顿第二定律应用于圆周运动,由于向心加速度表示不同,有以下各种情况,解题时应根据已知条件进行选择.
F = m = mrω2 = m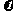 ω = mr
ω = mr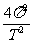 = 4π2mrf2
= 4π2mrf2
1.类平抛运动:
求解的方法是利用运动的合成和分解法进行分析:在初速度方向加速度为零,以初速度做匀速直线运动;在垂直于初速度方向有一个恒定的加速度,做静止开始的匀加速直线运动,加速度的大小由合外力决定.通常应结合运动的合成和分解的运动学规律进行求解.
23.(本小题满分10分)
模型拓展一:(1)1+5=6
(2)1+5×9=46
(3)1+5(n-1)
模型拓展二:(1)1+m
(2)1+m(n-1)
问题解决:(1)在不透明口袋中放入18种颜色的小球(小球除颜色外完全相同)各40个,现要确保从口袋中随机摸出的小球至少有10个是同色的,则最少需摸出多少个小球?
(2)1+18×(10-1) =163
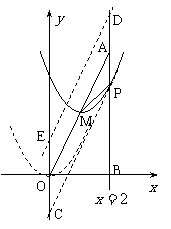
 18.(浙江省2008)如图,在平面直角坐标系中,已知点
18.(浙江省2008)如图,在平面直角坐标系中,已知点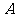 坐标为(2,4),直线
坐标为(2,4),直线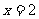 与
与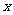 轴相交于点
轴相交于点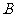 ,连结
,连结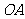 ,抛物线
,抛物线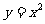 从点
从点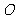 沿
沿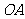 方向平移,与直线
方向平移,与直线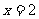 交于点
交于点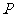 ,顶点
,顶点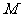 到
到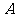 点时停止移动.
点时停止移动.
(1)求线段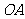 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点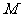 的横坐标为
的横坐标为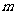 ,
,
①用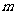 的代数式表示点
的代数式表示点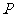 的坐标;
的坐标;
②当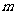 为何值时,线段
为何值时,线段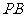 最短;
最短;
(3)当线段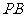 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点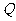 ,使△
,使△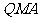
的面积与△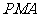 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点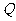 的坐标;若
的坐标;若
不存在,请说明理由.
解:(1)设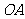 所在直线的函数解析式为
所在直线的函数解析式为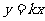 ,
,
∵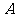 (2,4),
(2,4),
∴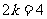 ,
, 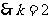 ,
,
∴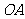 所在直线的函数解析式为
所在直线的函数解析式为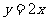 .
.
(2)①∵顶点M的横坐标为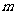 ,且在线段
,且在线段 上移动,
上移动,
∴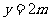 (0≤
(0≤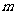 ≤2).
≤2).
∴顶点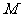 的坐标为(
的坐标为(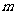 ,
,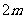 ).
).
∴抛物线函数解析式为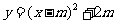 .
.
∴当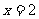 时,
时,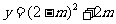
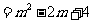 (0≤
(0≤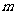 ≤2).
≤2).
∴点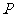 的坐标是(2,
的坐标是(2,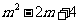 ).
).
② ∵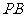 =
=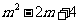 =
=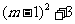 , 又∵0≤
, 又∵0≤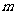 ≤2,
≤2,
∴当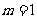 时,PB最短.
时,PB最短.
(3)当线段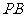 最短时,此时抛物线的解析式为
最短时,此时抛物线的解析式为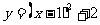 .
.
假设在抛物线上存在点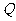 ,使
,使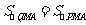 .
.
设点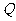 的坐标为(
的坐标为(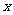 ,
,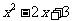 ).
).
①当点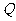 落在直线
落在直线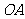 的下方时,过
的下方时,过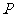 作直线
作直线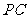 //
//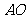 ,交
,交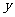 轴于点
轴于点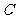 ,
,
∵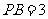 ,
,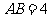 ,
,
∴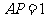 ,∴
,∴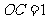 ,∴
,∴ 点的坐标是(0,
点的坐标是(0, ).
).
 ∵点
∵点 的坐标是(2,3),∴直线
的坐标是(2,3),∴直线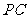 的函数解析式为
的函数解析式为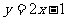 .
.
∵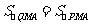 ,∴点
,∴点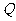 落在直线
落在直线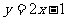 上.
上.
∴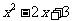 =
=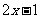 .
.
解得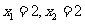 ,即点
,即点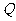 (2,3).
(2,3).
∴点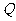 与点
与点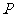 重合.
重合.
∴此时抛物线上不存在点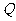 ,使△
,使△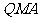 与△
与△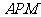 的面积
的面积
相等.
②当点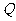 落在直线
落在直线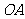 的上方时,
的上方时,
作点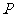 关于点
关于点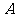 的对称称点
的对称称点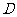 ,过
,过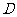 作直线
作直线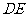 //
//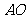 ,交
,交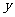 轴于点
轴于点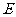 ,
,
∵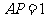 ,∴
,∴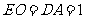 ,∴
,∴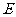 、
、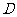 的坐标分别是(0,1),(2,5),
的坐标分别是(0,1),(2,5),
∴直线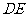 函数解析式为
函数解析式为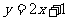 .
.
∵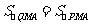 ,∴点
,∴点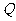 落在直线
落在直线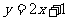 上.
上.
∴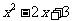 =
=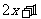 .
.
解得: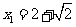 ,
,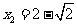 .
.
代入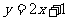 ,得
,得 ,
,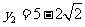 .
.
∴此时抛物线上存在点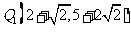 ,
,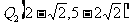
使△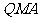 与△
与△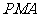 的面积相等.
的面积相等.
综上所述,抛物线上存在点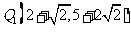 ,
,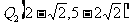
使△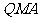 与△
与△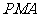 的面积相等.
的面积相等.
17.(青岛市2008)
实际问题:某学校共有18个教学班,每班的学生数都是40人.为了解学生课余时间上网情况,学校打算做一次抽样调查,如果要确保全校抽取出来的学生中至少有10人在同一班级,那么全校最少需抽取多少名学生?
建立模型:为解决上面的“实际问题”,我们先建立并研究下面从口袋中摸球的数学模型:
在不透明的口袋中装有红、黄、白三种颜色的小球各20个(除颜色外完全相同),现要确保从口袋中随机摸出的小球至少有10个是同色的,则最少需摸出多少个小球?
为了找到解决问题的办法,我们可把上述问题简单化:
(1)我们首先考虑最简单的情况:即要确保从口袋中摸出的小球至少有2个是同色的,则最少需摸出多少个小球?
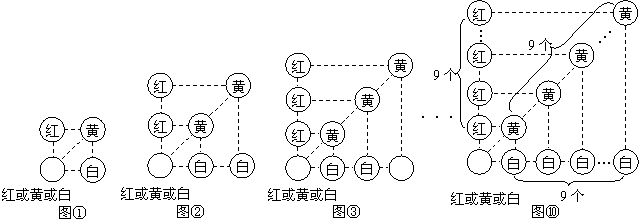
假若从袋中随机摸出3个小球,它们的颜色可能会出现多种情况,其中最不利的情况就是它们的颜色各不相同,那么只需再从袋中摸出1个小球就可确保至少有2个小球同色,即最少需摸出小球的个数是: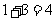 (如图①);
(如图①);
(2)若要确保从口袋中摸出的小球至少有3个是同色的呢?
我们只需在(1)的基础上,再从袋中摸出3个小球,就可确保至少有3个小球同色,即最少需摸出小球的个数是: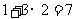 (如图②)
(如图②)
(3)若要确保从口袋中摸出的小球至少有4个是同色的呢?
我们只需在(2)的基础上,再从袋中摸出3个小球,就可确保至少有4个小球同色,即最少需摸出小球的个数是: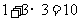 (如图③):
(如图③):

(10)若要确保从口袋中摸出的小球至少有10个是同色的呢?
我们只需在(9)的基础上,再从袋中摸出3个小球,就可确保至少有10个小球
同色,即最少需摸出小球的个数是: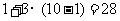 (如图⑩)
(如图⑩)
模型拓展一:在不透明的口袋中装有红、黄、白、蓝、绿五种颜色的小球各20分(除颜色外完全相同),现从袋中随机摸球:
(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是 ;
(2)若要确保摸出的小球至少有10个同色,则最少需摸出小球的个数是 ;
(3)若要确保摸出的小球至少有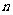 个同色(
个同色(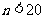 ),则最少需摸出小球的个数是 .
),则最少需摸出小球的个数是 .
模型拓展二:在不透明口袋中装有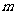 种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是 .
(2)若要确保摸出的小球至少有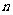 个同色(
个同色( ),则最少需摸出小球的个数是 .
),则最少需摸出小球的个数是 .
问题解决:(1)请把本题中的“实际问题”转化为一个从口袋中摸球的数学模型;
(2)根据(1)中建立的数学模型,求出全校最少需抽取多少名学生.
16.(湖北省十堰市2008 )
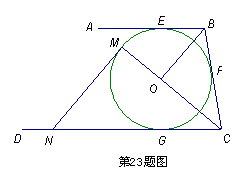
如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
⑴求证:MN是⊙O的切线;
⑵当0B=6cm,OC=8cm时,求⊙O的半径及MN的长.
解:⑴证明:∵AB、BC、CD分别与⊙O切于点E、F、G,
∴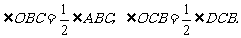
∵AB∥CD,∴∠ABC+∠DCB=180°.
∴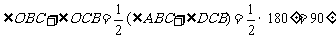
∴
∵MN∥OB,∴∠NMC=∠BOC=90°.∴MN是⊙O的切线.
⑵连接OF,则OF⊥BC.
由⑴知,△BOC是Rt△,∴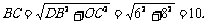
∵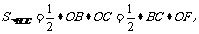
∴6×8=10×OF.∴0F=4.8.
即⊙O的半径为4.8cm.
由⑴知,∠NCM=∠BCO,∠NMC=∠BOC=90°,
∴△NMC∽△BOC.
∴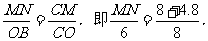
∴MN=9.6(cm).
说明:不带单位不扣分.
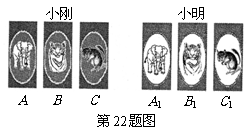
14.(沈阳市2008)小刚和小明两位同学玩一种游戏.游戏规则为:两人各执“象、虎、鼠”三张牌,同时各出一张牌定胜负,其中象胜虎、虎胜鼠、鼠胜象,若两人所出牌相同,则为平局.例如,小刚出象牌,小明出虎牌,则小刚胜;又如,两人同时出象牌,则两人平局.
(1)一次出牌小刚出“象”牌的概率是多少?
 (2)如果用
(2)如果用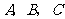 分别表示小刚的象、虎、鼠三张牌,用
分别表示小刚的象、虎、鼠三张牌,用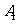 ,
,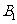 ,
,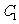 分别表示小明的象、虎、鼠三张牌,那么一次出牌小刚胜小明的概率是多少?用列表法或画树状图(树形图)法加以说明.
分别表示小明的象、虎、鼠三张牌,那么一次出牌小刚胜小明的概率是多少?用列表法或画树状图(树形图)法加以说明.
解:(1)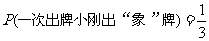
(2)树状图(树形图):


或列表
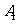
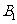
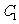
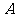
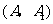
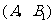
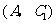
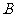
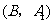
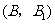
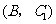
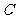
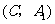
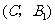
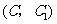
由树状图(树形图)或列表可知,可能出现的结果有9种,而且每种结果出现的可能性相同,其中小刚胜小明的结果有3种.
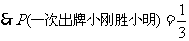 .
.
15(山东省2008)
如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向、点B的北偏东30°方向上,AB=2km,∠DAC=15°.
(1)求B,D之间的距离;
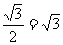 ,BO=2×cos60°=1.
,BO=2×cos60°=1.
在Rt△CBO中,∠CBO=30°,CO=BOtan30°=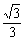 ,
,
∴ CD=DO-CO=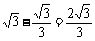 (km).
(km).
即C,D之间的距离为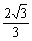 km.
km.
13.(浙江省2008)四川5.12特大地震受灾地区急需大量赈灾帐篷,某帐篷生产企业接到生产任务后,加大生产投入、提高生产效率,实际每天生产帐篷比原计划多200顶,已知现在生产3000顶帐篷所用的时间与原计划生产2000顶的时间相同.现在该企业每天能生产多少顶帐篷?
解:设现在该企业每天能生产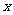 顶帐篷,
顶帐篷,
则原计划每天生产(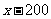 )顶帐篷.
)顶帐篷.
由题意,得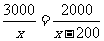 .
.
解得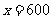 .
.
经检验: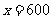 是原方程的解.
是原方程的解.
∴原方程的解是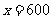 .
.
答:现在该企业每天能生产 顶帐篷.
顶帐篷.
12.(四川省达州市2008)含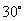 角的直角三角板
角的直角三角板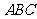 (
(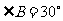 )绕直角顶点
)绕直角顶点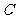 沿逆时针方向旋转角
沿逆时针方向旋转角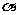 (
(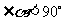 ),再沿
),再沿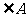 的对边翻折得到
的对边翻折得到 ,
,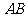 与
与 交于点
交于点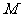 ,
, 与
与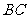 交于点
交于点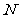 ,
, 与
与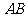 相交于点
相交于点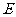 .
.
(1)求证: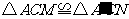 .
.
(2)当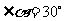 时,找出
时,找出 与
与 的数量关系,并加以说明.
的数量关系,并加以说明.
(1) 证明:∵∠A=∠A′ AC=A′C ∠ACM=∠A′CN=900-∠MCN
∴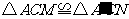
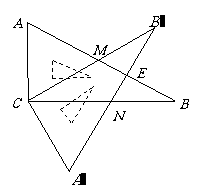 (2)在Rt△ABC中
(2)在Rt△ABC中
∵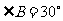 ,∴∠A=900-300=600
,∴∠A=900-300=600
又∵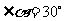 ,∴∠MCN=300,
,∴∠MCN=300,
∴∠ACM=900-∠MCN=600
∴∠EMB′=∠AMC=∠A=∠MCA=600
∵∠B′=∠B=300
所以三角形MEB′是Rt△MEB′且∠B′=300
所以MB′=2ME
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com