
8、以:⑴以啮人:假设连词:如果⑵皆以美于徐公:认为⑶不以疾也: 如⑷可以为师矣:凭借⑸可以一战:凭借(6)何以谓之“文”也:凭⑺不以臣卑鄙:因为⑻以其境过清:因为⑼以中又足乐者:因为⑽不以物喜:因为⑾属予作文以记之:来⑿无从致书以观:来⒀余故道为学之难以告之:来⒁以光先帝遗德:来⒂以昭陛下平明之理:来⒃以彰其咎:来⒄以咨诹善道:来⒅以塞忠谏之路:以致⒆以伤先帝之明:以致⒇必以分人:把(21)故临崩寄臣以大事也:把(22)托臣以讨贼兴复之效:把(23)以手拂之:用(24)以衾拥覆:用(25)醒能述以文者:用(26)以乡人子谒余:用(27)必以情:根据(28)策之不以其道:按照,根据(29)以备一板内有重复者:用来(30)计日以还:相当于“而”,不译(31)俯身倾耳以请:相当于“而”,可译作“地”(32)卷石底以出:相当于“而”,表承接,不译
7、于:⑴所欲有甚于生者:比⑵皆以美于徐公:比⑶降大任于是人也:给⑷万钟于我何加焉:对于,对⑸临于泉上者:在(6)生于忧患:在⑺苟全性命于乱世:在⑻奉命于危难之间:在⑼此所谓战胜于朝廷:在⑽还于旧都:到⑾皆朝于齐:到⑿三顾臣于草庐之中:到⒀泻出于两峰之间者:从⒁发于畎亩之中(举于士):从⒂有求于我也:对
6、盖:⑴盖竹柏影也:原来是⑵盖简桃核修狭者为之:原来是⑶盖余之勤且艰若此:大概⑷盖追先帝之殊遇:副词,推测原因⑸盖大苏泛赤壁云:刻的原来是
5、为:⑴或异二者之为:心理活动(即两种心情)⑵为宫室之美:为了⑶不足为外人道也:对,向⑷一一为具言所闻:给⑸武陵人捕鱼为业:作为(6)其印为予群从所得:被⑺又为活板:发明⑻为宫室器皿:雕刻⑼以后典籍皆为板本:是⑽若是佣耕:是⑾则极为神速:算是⑿未为简易:算是
4、虽⑴虽乘奔御风:即使⑵虽人有百口:即使⑶故虽有名马:即使⑷⑸虽有千里之能:虽然(6)故余虽愚:虽然⑺虽不能察:虽然
3、则:⑴入则无法家拂士:如果⑵万钟则不辩礼义而受之:如果⑶问之,则曰:却⑷余则 袍敝衣处其间:却⑸则素湍绿潭:表轻微的转折。(6)则吾斯役之不幸: 转折连词,然而,可是⑺然则:那么⑻此则岳阳楼之大观也:就是⑼有仙则名:就
2、乎:⑴吾尝疑乎是:介词,对于⑵颓然乎其间:介词,在⑶叫嚣乎东西:介词,在⑷若毒之乎:语气助词,吗
1、焉:⑴必有我师焉:于之,在里面⑵惧有伏焉:于之,在那里⑶不复出焉:于之,从这里⑷争奔走焉:指捕蛇这个差事,有语气词兼代词的作用⑸时而献焉:代指蛇(6)观人风者得焉:代这篇文章⑺虽鸡狗不得宁焉:语气助词,啊⑻有子存焉:语气助词⑼且焉置土石:疑问代词,哪里。
4.解题途径:
 当物体在两个共点力作用下平衡时,这两个力一定等值反向;当物体在三个共点力作用下平衡时,往往采用平行四边形定则或三角形定则;当物体在四个或四个以上共点力作用下平衡时,往往采用正交分解法。
当物体在两个共点力作用下平衡时,这两个力一定等值反向;当物体在三个共点力作用下平衡时,往往采用平行四边形定则或三角形定则;当物体在四个或四个以上共点力作用下平衡时,往往采用正交分解法。
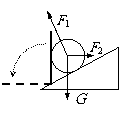
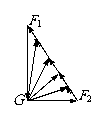
[例13]重G的光滑小球静止在固定斜面和竖直挡板之间。若挡板逆时针缓慢转到水平位置,在该过程中,斜面和挡板对小球的弹力的大小F1、F2各如何变化?
解:由于挡板是缓慢转动的,可以认为每个时刻小球都处于静止状态,因此所受合力为零。应用三角形定则,G、F1、F2三个矢量应组成封闭三角形,其中G的大小、方向始终保持不变;F1的方向不变;F2的起点在G的终点处,而终点必须在F1所在的直线上,由作图可知,挡板逆时针转动90°过程,F2矢量也逆时针转动90°,因此F1逐渐变小,F2先变小后变大。(当F2⊥F1,即挡板与斜面垂直时,F2最小)
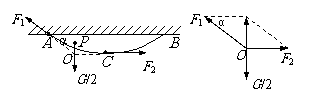 [例14]重G的均匀绳两端悬于水平天花板上的A、B两点。静止时绳两端的切线方向与天花板成α角。求绳的A端所受拉力F1和绳中点C处的张力F2。
[例14]重G的均匀绳两端悬于水平天花板上的A、B两点。静止时绳两端的切线方向与天花板成α角。求绳的A端所受拉力F1和绳中点C处的张力F2。
解:以AC段绳为研究对象,根据判定定理,虽然AC所受的三个力分别作用在不同的点(如图中的A、C、P点),但它们必为共点力。设它们延长线的交点为O,用平行四边形定则作图可得: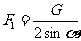 ,
,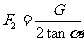 。
。
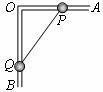
[例15]有一个直角支架AOB,AO水平放置,表面粗糙, OB竖直向下,表面光滑。AO上套有小环P,OB上套有小环Q,两环质量均为m,两环由一根质量可忽略、不可伸长的细绳相连,并在某一位置平衡(如图所示)。现将P环向左移一小段距离,两环再次达到平衡,那么将移动后的平衡状态和原来的平衡状态比较,AO杆对P环的支持力FN和摩擦力f的变化情况是
 A.FN不变,f变大
B.FN不变,f变小
A.FN不变,f变大
B.FN不变,f变小
 C.FN变大,f变大
D.FN变大,f变小
C.FN变大,f变大
D.FN变大,f变小
解:以两环和细绳整体为对象求FN,可知竖直方向上始终二力平衡,FN=2mg不变;以Q环为对象,在重力、细绳拉力F和OB压力N作用下平衡,设细绳和竖直方向的夹角为α,则P环向左移的过程中α将减小,N=mgtanα也将减小。再以整体为对象,水平方向只有OB对Q的压力N和OA 对P环的摩擦力f作用,因此f=N也减小。答案选B。
[例16]A的质量是m,A、B始终相对静止,共同沿水平面向右运动。当a1=0和a2=0.75g时,B对A的作用力FB各多大?
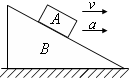 解:一定要审清题:B对A的作用力FB是B对A的支持力和摩擦力的合力。而A所受重力G=mg和FB的合力是F=ma。
解:一定要审清题:B对A的作用力FB是B对A的支持力和摩擦力的合力。而A所受重力G=mg和FB的合力是F=ma。
当a1=0时,G与 FB二力平衡,所以FB大小为mg,方向竖直向上。
当a2=0.75g时,用平行四边形定则作图:先画出重力(大小和方向),再画出A所受合力F的大小和方向,再根据平行四边形定则画出FB。由已知可得FB的大小FB=1.25mg,方向与竖直方向成370角斜向右上方。
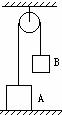 [例17] 如图所示,两物体A和B,质量分别为M和m。用跨过定滑轮的轻绳相连,A静止于水平地面上,不计定滑轮与各个接触物体之间的摩擦。物体A对轻绳的作用力的大小和地面对物体A的作用力的大小分别是多少?
[例17] 如图所示,两物体A和B,质量分别为M和m。用跨过定滑轮的轻绳相连,A静止于水平地面上,不计定滑轮与各个接触物体之间的摩擦。物体A对轻绳的作用力的大小和地面对物体A的作用力的大小分别是多少?
分析与解答:本题的关键词语有:“静止”、“轻绳”、“不计……摩擦”。
对B进行受力分析:竖直向下的重力和竖直的向上轻绳对物体B的拉力。
对A进行受力分析:竖直向下的重力、竖直向上的轻绳对物体A的拉力和竖直向上的地面对物体A的支持力。其中轻绳对物体A和轻绳对物体B的拉力是相等的。
根据物体A和物体B都处于静止状态可知,轻绳对物体B的拉力等于物体B的重力;轻绳对物体B的拉力等于物体B对轻绳的拉力(这是一对作用力和反作用力),轻绳对物体A的作用力等于轻绳中的张力,即等于物体B的重力。
对于物体A,根据平衡知识可知,物体A受到的重力等于轻绳对物体A的拉力与地面对物体A的支持力的和。又轻绳对物体A的拉力等于物体B的重力,所以,地面对物体A的支持力等于物体A的重力减去轻绳对物体A的拉力,即等于物体A的重力减去物体B的重力。
[续问](1)物体A对地面的压力(等于地面对物体A的支持力);(2)物体B对轻绳的拉力(等于物体B的重力);(3)另一段轻绳对天花板的拉力(等于两倍物体B的重力)。
[变形]连接物体A的轻绳与竖直线之间有一夹角θ,整个装置仍处于静止状态。
这时轻绳中的拉力仍等于物体B的重力,物体A将受到地面水平方向的摩擦力作用,大小等于物体B的重力乘以θ角的正弦;地面对物体A的支持力等于物体A受到的重力减去物体B的重力与θ角的余弦的积。地面对物体A的作用力自己可以推导;若定滑轮的质量不计,还可以求另一段轻绳对天花板的作用力的大小和方向{方向与竖直线的夹角为θ/2;大小为2mgcos(θ/2)}。
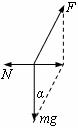
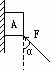 [例18]重力为G的物体A受到与竖直方向成α角的外力F后,静止在竖直墙面上,如图所示,试求墙对物体A的静摩擦力。
[例18]重力为G的物体A受到与竖直方向成α角的外力F后,静止在竖直墙面上,如图所示,试求墙对物体A的静摩擦力。
分析与解答:
这是物体静力平衡问题。首先确定研究对象,对研究对象进行受力分析,画出受力图。A受竖直向下的重力G,外力F,墙对A水平向右的支持力N,以及还可能有静摩擦力f。这里对静摩擦力的有无及方向的判断是极其重要的。物体之间有相对运动趋势时,它们之间就有静摩擦力;物体间没有相对运动趋势时,它们之间就没有静摩擦力。那么有无静摩擦力的鉴别,关键是对相对运动趋势的理解。我们可以假设接触面是光滑的,若不会相对运动,物体将不受静摩擦力,若有相对运动就有静摩擦力。
(注意:这种假设的方法在研究物理问题时是常用的方法,也是很重要的方法。)
正确的答案应该是:
当 Fcosα=G时,物体A在竖直方向上受力已经平衡,故静摩擦力为零;
当 Fcosα<G时,物体有向下滑动的趋势,故静摩擦力f的方向向上,大小为G-F·cosα;
当 Fcosα>G时,物体有向上滑动的趋势,故静摩擦力f的方向向下,大小为 Fcosα-G。
注意:墙对物体的支持力为N,N=F·sinα,但不能用f=μN来计算静摩擦力。f=μN只适用于滑动摩擦力的计算,在高中学习的范围,我们认为最大静摩擦力与滑动摩擦力相等。
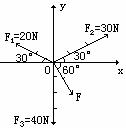
[例19]如图示,大小为20N、30N和40N的三个力作用于物体一点上,夹角互为120°,求合力的大小和方向。
分析与解答:不在一条直线上的共点力合成应遵从平行四边形法则。
方法一:设F1=20N,F2=30N,F3=40N,可用代数法(公式法)求解。先求出F1和F2的合力F12的大小和方向,然后再将F12与F3合成求出大小和方向,此法计算准确误差小但过于繁杂。
方法二:利用作图法求解,没有繁杂的计算,但作图误差不可避免,大小和方向都会产生误差。
方法三:可用分解后再合成,化复杂为简单,选取平面直角坐标系如图所示。将F2、F1沿坐标轴方向分解[分解的矢量越少越好,这就是选取坐标系的原则]:
 ΣFx=F1x+F2x+F3x=-F1cos30°+F2cos30°+0=-20×
ΣFx=F1x+F2x+F3x=-F1cos30°+F2cos30°+0=-20×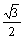 +30×
+30×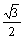 =5
=5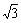 N
N
ΣFy=F1y+F2y+F3y=-F1sin30°+F2sin30°-F3=20×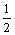 +30×
+30×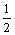 -40=-15N
-40=-15N
∑F=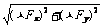 =
=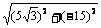 =10
=10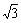 N
N
tanθ=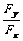 =
=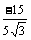 =
=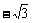 ,即θ=-600
,即θ=-600
F与x轴正方向夹角为600,如图所示。
方法四:利用已知的结论进行解题往往更简捷,特别是在填空、选择题中发挥明显的优势。
三个大小相等互为120°角的三个共点力的合力为零,这一点很容易证明,如果我们把F2、F3中的20N与F1进行合成,合力便为零,此题就简化为一个10N和一个20N的两个力夹角为120°的合成问题,这时不管是用计算法还是作图法都会觉得很方便且容易得多。
 方法五:若仍用方法四中的思路,而是每个力中取30N,F3则再将加上-10N,F1再加10N即可,这样此题就简化成两个夹角为60°、大小均为10N的两个力的合成问题,利用直角三角形的知识即可解决,不必经分解后再合成的迂回步骤。可见一题多解是训练思维的好方法,是提高能力的有效措施。
方法五:若仍用方法四中的思路,而是每个力中取30N,F3则再将加上-10N,F1再加10N即可,这样此题就简化成两个夹角为60°、大小均为10N的两个力的合成问题,利用直角三角形的知识即可解决,不必经分解后再合成的迂回步骤。可见一题多解是训练思维的好方法,是提高能力的有效措施。
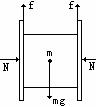
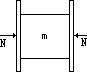
[例20]如图所示,一块木块被两块木板夹在中间静止不动,在两侧对两木板所加水平方向力的大小均为N,木块的质量为m。
(1)木块与木板间的静摩擦力是多少?
(2)若木块与木板间的最大静摩擦系数为μ,欲将木块向下或向上抽出,则所需的外力F各多大?
分析与解答:
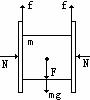 (1)由于木块处于平衡状态,且木块两侧均分别与木板接触,所以木块两侧均受向上的静摩擦力,其大小的总和与重力相等,如图所示,即2f=mg,所以木块与木板间的静摩擦力为f=mg/2。
(1)由于木块处于平衡状态,且木块两侧均分别与木板接触,所以木块两侧均受向上的静摩擦力,其大小的总和与重力相等,如图所示,即2f=mg,所以木块与木板间的静摩擦力为f=mg/2。
(2)若对木块施加一向下的外力F,木块仍处于平衡状态,则木块所受的静摩擦力方向仍向上,且随着外力F的增大而增大,如图所示。当静摩擦力增大到最大静摩擦力时,本块开始相对于木板滑动,这时可将木块从木板中抽出,有:F+mg=2fmax,其中fmax为最大静摩擦力,且fmax=μN,所以F=2μN-mg。
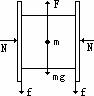 (3)当对木块加一向上的力F时,开始木块所受静摩擦力方向向上,且随F的增加而减小。当F增大到一定值时,恰好使木块的静摩擦力为零。这时若F继续增加,则木块受的静摩擦力向下,且随F的增大而增大,当F增大到一定程度,木块的静摩擦力为最大静摩擦力,这时,木块将被向上抽出,如图所示。有:F=mg+2fmax,其中fmax为最大静摩擦力,且fmax=μN,所以F=mg+2μN。
(3)当对木块加一向上的力F时,开始木块所受静摩擦力方向向上,且随F的增加而减小。当F增大到一定值时,恰好使木块的静摩擦力为零。这时若F继续增加,则木块受的静摩擦力向下,且随F的增大而增大,当F增大到一定程度,木块的静摩擦力为最大静摩擦力,这时,木块将被向上抽出,如图所示。有:F=mg+2fmax,其中fmax为最大静摩擦力,且fmax=μN,所以F=mg+2μN。
所以欲将木块向下抽出,至少需加2μN-mg的外力,欲将木块向上抽出,至少需加2μN+mg的外力。
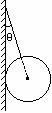
[例21]用绳将球A挂在光滑竖直墙上,如图所示。(1)现施加外力将球A绕球心顺时针转过一个小角度,外力撤去后,球的运动情况如何?(2)墙面光滑,绳子变短时,绳的拉力和球对墙的压力将如何变化?
分析与解答:
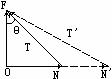
(1)因为墙是光滑的,绳子的作用力一定过球心。取球为研究对象,受力图如图所示。N为墙对球的力,方向水平向右;重力mg方向竖直向下;绳拉力T沿绳的方向,θ为绳与墙的夹角。因为小球静止,所以N、T、mg的合力为零,即T、N的合力F大小等于mg,方向竖直向上,T=mg/cosθ,N=mgtanθ。
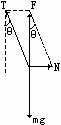 当球A受到外力矩使其顺时针转动一个小角度后,重力mg和墙对球的支持力方向不变且均过球心,而绳对球A的作用力T不再过球心,且此力T对球A中心产生一使球A逆时针转动的效果,墙面光滑无摩擦力。所以外力撤去后,球A在力T对球A的作用下使球A绕球心逆时针转动。当球A转动到原平衡位置时,球A具有转动动能而继续转动,转动到一定角度后速度为零,而后球A向顺时针方向转动,再次转动到平衡位置时,球A仍具有转动动能而继续顺时针方向转动,转动为速度为零后又重复上述过程。
当球A受到外力矩使其顺时针转动一个小角度后,重力mg和墙对球的支持力方向不变且均过球心,而绳对球A的作用力T不再过球心,且此力T对球A中心产生一使球A逆时针转动的效果,墙面光滑无摩擦力。所以外力撤去后,球A在力T对球A的作用下使球A绕球心逆时针转动。当球A转动到原平衡位置时,球A具有转动动能而继续转动,转动到一定角度后速度为零,而后球A向顺时针方向转动,再次转动到平衡位置时,球A仍具有转动动能而继续顺时针方向转动,转动为速度为零后又重复上述过程。
(2)研究变量的问题,我们要紧紧抓住被研究变量与不变量之间的关系,这是研究此类问题的一般思路和方法.由受力图可知:
T=mg/cosθ ①
 N=mgtanθ ②
N=mgtanθ ②
墙面光滑,当绳子变短时,θ角增大,式①中cosθ将变小,但其在分母上故整个分式变大,即T增大;式②中tanθ随θ变大而增大,故N也增大。
此题也可用图解法求解,因为T、N的合力F大小为mg,方向竖直向上,N的方向也已知总是垂直于墙(这些都是不变的量)。即已知合力和一个分力的方向求另一个分力。根据矢量合成的三角形法则,由图可知,当θ增大时,N变为N′,T变为T′,都将增大。
3.三力汇交原理:物体在三个互不平行的力的作用下处于平衡,则这三个力必为共点力。(表示这三个力的矢量首尾相接,恰能组成一个封闭三角形)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com