61．在解三角问题时，你注意到正切函数、余切函数的定义域了吗？你注意到正弦函数、余弦函数的有界性了吗？在△ABC中，sinA>sinBÛA>B对吗? 例：已知直线是函数(其中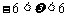)的图象的一条对称轴，则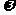的值是　　　 。()

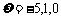60．样本中心位置特征数(平均数、中位数、众数)与离散程度特征数(标准差、方差)有何用处？(例如：(1)给出下列四种说法：① 3，3，4，4，5，5，5的众数是5；② 3，3，4，4，5，5，5的中位数是4.5；③ 频率分布直方图中每一个小长方形的面积等于该组的频率；

④ 频率分布表中各小组的频数之和等于1.其中说法正确的序号依次是　　　　　　　 .

(2) 甲乙两种棉花苗中各抽10株, 测得它们的株高分别如下(单位:cm)

　 甲: 25,41,40,37,22,14,19,39,21,42　　 乙: 27,16,44,27,44,16,40,40,16,40

(1)估计两种棉花苗总体的长势:哪种长的高一些?　 (2)哪种棉花的苗长得整齐一些?)

(必修4)

59．运用互斥事件的概率加法公式时，首先要判断它们是否互斥，再由随机事件的概率公式分别求它们的概率，然后计算。在计算某些事件的概率较复杂时，可转化为对立事件的概率。例如：在10件产品中，有8件是合格的，2件是次品，从中任意抽2件进行检验，计算：(i)两件都是次品的概率；(ii)2件中恰好有一件是合格品的概率；(iii)至多有一件是合格品的概率

58．古典概型与几何概型的计算公式分别是什么？

古典概型：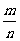　　　　　

　P(A)=　　　　　　　　　　　　　　　　　　

例如：(1)玻璃球盒中装有各色球12只，其中5红、4黑、2白、1绿. (i)从中取1个球, 求取得红或白的概率. (ii)若从中取2个球，求至少一个红球的概率.

几何概型：若记事件A={任取一个样本点，它落在区域g}，则A的概率定义为

．

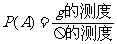例如：甲乙两人相约某天在某地点见面，甲计划在上午8：30至9：30之间到达，乙计划在上午9：00至10：00之间到达. (i)求甲比乙提前到达的概率； (ii)如果其中一人先到达后最多等候另一人15分钟，然后离去. 求两人能够会面的概率.

57．应用直线回归的注意事项(1)做回归分析要有实际意义；(2)回归分析前,最好先作出散点图；(3)回归直线不要外延；(4)回归直线都经过样本中心点。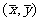

例如：由一组样本数据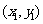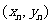，，，得到回归直线方程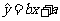，那么下列说法中不正确的是(　B　)

A．直线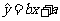必经过点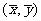　

　B．直线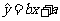至少经过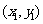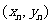点，，，中的一个点

C．直线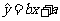的斜率为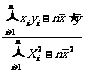

D．直线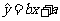的纵截距为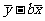

56．如何利用最小二乘法求解回归方程？最小二乘法的思想是什么？求出直线回归方程有何用处？

(1)描述两变量之间的依存关系；利用直线回归方程即可定量描述两个变量间依存的数量关系;

(2)利用回归方程进行预测；把预报因子(即自变量x)代入回归方程对预报量(即因变量Y)进行估计，即可得到个体Y值的容许区间。

(3)利用回归方程进行统计控制规定Y值的变化，通过控制x的范围来实现统计控制的目标。如:已经得到了空气中NO₂的浓度和汽车流量间的回归方程，即可通过控制汽车流量来控制空气中NO₂的浓度。

55．你知道如何判断两个变量是否存在线性相关关系吗？(①.利用散点图可以粗略地判断；②.利用相关系数)相关系数越大，两变量的相关性是否就越大？

54．频率分布直方图中每一个小矩形的面积等于数据落在相应区间上的频率，所有小矩形的

面积之和等于1.

53．什么是进位制？不同的进位制之间又有什么联系呢？它们之间如何进行转换？

2.这种算法在计算时共用了多少次乘法运算？多少次加法运算？此方案有何优缺点？

解:上述算法一共做了5+4+3+2+1＝15次乘法运算，5次加法运算. 优点是简单、易懂；缺点是不通用，不能解决任意多项式的求值问题，而且计算效率不高.

若用秦九韶算法计算时共用了多少次乘法运算？多少次加法运算？此方案有何优缺点？

解:上述算法一共做了4次乘法运算，5次加法运算)秦九韶算法将求次多项式的值转化为求个一次多项式的值，整个过程只需次乘法运算和次加法运算；观察上述个一次式，可发出的计算要用到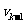的值，若令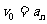，可得到下列递推公式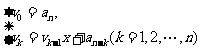：. 这是一个反复执行的步骤，因此可用循环结构来实现.