130．你知道复数的几何意义吗？

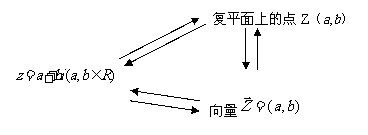
复数对应了复平面上的一个点，而点的坐标又对应了一个向量，因此复数在复数面上的对应关系如右图所示：

129．(理)你掌握数学归纳法证明数学问题的步骤了吗？

128．反证法主要用来证明什么样的问题？

反证法常用于证明如下形式的问题：否定性问题、存在性问题、唯一性问题，至多、至少问题，结论的反面比原结论更具体更易于研究和掌握的问题。

127．关于空间问题与平面问题的类比，通常可抓住几何要素的如下对应关系作对比：

　多面体　　　　 多边形；　　　　　 面　　　　　 边

　　　　 体 积　　　　　 面 积 ；　　　　 二面角　　　　 平面角

　　　　 面 积　　　　　 线段长；　　　　　 … ….

126．(理) 定积分的性质有何用处？(运用定积分的性质可以将较为复杂的求定积分问题转化为简单的求定积分问题，因此，在求定积分时应充分考虑利用定积分的性质化简后再进行求解)

125．导数为0的点不一定都是极值点，(即=0是函数y=f(x)在x=x₀处有极值的必要不充分条件。

例如：y=x³,当x=0时，导数是0，但非极值点。导数为0的点是否是极值点，取决于这个点左、右两边的增减性，即两边的y′的符号，若改变符号，则该点为极值点；若不改变符号，则非极值点，一个函数的极值点不一定在导数为0的点处取得，但可得函数的极值点一定导数为0.

124．导数的主要应用是什么？

导数的应用主要包括以下几个方面:(1)利用导数研究函数的单调性和单调区间;(2)利用导数研究函数极值与最值;(3)利用导数研究曲线的切线问题;(4)利用导数研究不等式的证明问题;(5)利用导数研究函数的零点;(6)利用导数求参数的取值范围等.

123．求曲线的切线时，关键点在何处？(关键是寻找切点)求函数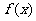图象上点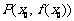处的切线方程的关键在于确定该点切线处的斜率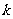，由导数的几何意义知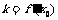，(注意曲线上某点处的导数值就是切线的斜率。(导数的几何意义))故当存在时，切线方程为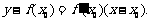求曲线的切线要注意“过点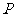的切线”与“点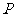处的切线”的差异.过点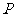的切线中，点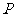不一定是切点，点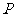也不一定在已知曲线上；点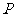处的切线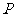，点是切点。

122．导数公式你记清了吗？(理)对复合函数的该如何求导？(①和与差的导数等于导数的和与差；②乘法的求导：前导后不导，后导前不导，中间是正号；③除法的求导：分母平方要记牢，上导下不导，下导上不导，中间是负号)(理) 复合函数的求导问题是个难点，要分清中间变量与复合关系，复合函数求导法则，像链条一样，必须一环一环套下去，而不能丢掉其中的一环. 防止漏掉一部分或漏掉符号造成错误.必须正确分析复合函数是由哪些基本函数经过怎样的顺序复合而成的，分清其间的复合关系.

121．导数的概念你理解了吗？导数有些什么应用。(理)定积分的概念与应用应注意.

① 了解函数单调性和导数的关系；能利用导数研究函数的单调性，会求函数的单调区间，对多项式函数一般不超过三次. ② 了解函数在某点取得极值的必要条件和充分条件；会用导数求函数的极大值、极小值，对多项式函数一般不超过三次；会求闭区间上函数的最大值、最小值，对多项式函数一般不超过三次.