
1.下列各组词语中加点字的注音和字形完全正确 一组是( )(2分)
A.暝想(míng) 隘口(ài) 竹篙(gǎo) 赡养(shàn)
B.簸箕(ji) 纨绔(kù) 毗邻(pí) 恣睢(zì)
C.祈祷(qǐ) 慰藉(jiè) 剔除(tī) 困恶(è)
D.骨髓(suǐ) 创伤(chuàng) 熟稔(rěn) 机械(xiè)
2.对下列句子中加点词语使用的错误,分析有问题的一项是( )
A. 我们班的语文科代表对工作尽职尽责,同学们都很爱戴他。
爱戴:敬爱并且拥护。适用于晚辈对长辈,下级对上级。
分析:对工作尽职尽责是值得学习的事情,谈不上“敬爱”和“拥护”。科代表是同学,不是长辈和上级,所以使用有误。
B. 昨天我做作业时遇到了一个难题,就对同桌说:“我不耻下问,向你请教一个问题,可以吗?”
不耻下问:不以向学问比自己差或地位、辈份比自己低的人请教为可耻。含褒义,形容虚心求教。
分析:同桌的学问未必比自己低,地位、辈份是平等的,所以使用有误。
C. 在外漂泊十多年的他见到亲人时终于忍俊不禁,流下了辛酸的眼泪。
忍俊不禁:原指热衷于某事,不能克制自己。后指忍不住发笑。
分析:久别重逢时“流下了辛酸的眼泪”,表明心里很不好受,应该是笑不出来的,所以使用有误。
D. 上次作文,王平同学因用词不当丢了丑以后,我决心吃一堑,长一智,苦下功夫背词造句,一定不要吃他那样的亏。
吃一堑,长一智:经受一次挫折,就会增长一分智慧。
分析:“经受一次挫折,就会增长一分智慧。”是从自己的角度说的,不是指吸取他人的经验教训,所以使用有误。
1.下列词语中加点字读音有误的是( )
A.勉强(qiǎng) 比拟(nǐ) 水涨船高(zhǎng)
B.膝盖(xī) 追溯(sù) 谆谆教诲(huì)
C.炫耀(xuàn) 赈灾(zhèn) 装模作样(mó)
D.称职(chèn) 狭隘(ài) 鲜为人知(xiǎn)
2.下列词语没有错别字的一项是( )
A.吵作 忙碌 娇嫩 再接再厉
B.游弋 陪伴 琐屑 历历在目
C. 急燥 安祥 阴晦 声色俱厉
D.联袂 掺扶 犀利 变本加利
1.下列词语中加点字的读音完全正确的一项是 ( )
A.惩罚(chéng) 堤岸(dī) 称心如意(chèng)
B.涨红(zhàng) 脑髓(suǐ) 扣人心弦(xuán)
C.胆怯(qiè) 教诲(huì) 随声附和(hè)
D.允许(rǔn) 憎恶(è) 一碧万顷(qǐng)
2. 田万海主编 数学教育学 浙江 浙江教育出版社 1993
庄亚栋主编 高中数学教与学(99.2、99.6) 扬州 中学数学教与学编辑部出版 1999
判断函数的奇偶性,应先考虑该函数的定义域区间是否关于坐标原点成中心对称,如果定义域区间是关于坐标原点不成中心对称,则函数就无奇偶性可谈。否则要用奇偶性定义加以判断。如:
例5:判断函数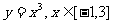 的奇偶性.
的奇偶性.
解:∵ 
∴ 定义域区间[-1,3]关于坐标原点不对称
∴ 函数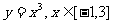 是非奇非偶函数.
是非奇非偶函数.
若学生像以上这样的过程解完这道题目,就很好地体现出学生解题思维的敏捷性
如果学生不注意函数定义域,那么判断函数的奇偶性得出如下错误结论:
∵ 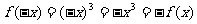
∴ 函数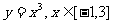 是奇函数.
是奇函数.
错误剖析:因为以上做法是没有判断该函数的定义域区间是否关于原点成中心对称的前提下直接加以判断所造成,这是学生极易忽视的步骤,也是造成结论错误的原因。
综上所述,在求解函数函数关系式、最值(值域)、单调性、奇偶性等问题中,若能精细地检查思维过程,思辨函数定义域有无改变(指对定义域为R来说),对解题结果有无影响,就能提高学生质疑辨析能力,有利于培养学生的思维品质,从而不断提高学生思维能力,进而有利于培养学生思维的创造性。
参 考 文 献
1. 王岳庭主编 数学教师的素质与中学生数学素质的培养论文集 北京 海洋出版社 1998
函数单调性是指函数在给定的定义域区间上函数自变量增加时,函数值随着增减的情况,所以讨论函数单调性必须在给定的定义域区间上进行。如:
例4:指出函数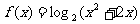 的单调区间.
的单调区间.
解:先求定义域:
∵
 ∴
∴
∴
函数定义域为 .
.
令 ,知在
,知在 上时,u为减函数,
上时,u为减函数,
在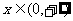 上时, u为增函数。
上时, u为增函数。
又∵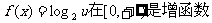 .
.
∴函数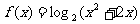 在
在 上是减函数,在
上是减函数,在 上是增函数。
上是增函数。
即函数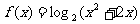 的单调递增区间
的单调递增区间 ,单调递减区间是
,单调递减区间是 。
。
如果在做题时,没有在定义域的两个区间上分别考虑函数的单调性,就说明学生对函数单调性的概念一知半解,没有理解,在做练习或作业时,只是对题型,套公式,而不去领会解题方法的实质,也说明学生的思维缺乏深刻性。
函数的值域是该函数全体函数值的集合,当定义域和对应法则确定,函数值也随之而定。因此在求函数值域时,应注意函数定义域。如:
例3:求函数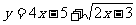 的值域.
的值域.
错解:令
∴
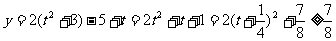
故所求的函数值域是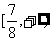 .
.
剖析:经换元后,应有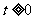 ,而函数
,而函数 在[0,+∞)上是增函数,
在[0,+∞)上是增函数,
所以当t=0时,ymin=1.
故所求的函数值域是[1, +∞).
以上例子说明,变量的允许值范围是何等的重要,若能发现变量隐含的取值范围,精细地检查解题思维的过程,就可以避免以上错误结果的产生。也就是说,学生若能在解好题目后,检验已经得到的结果,善于找出和改正自己的错误,善于精细地检查思维过程,便体现出良好的思维批判性。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com