
17. 已知等比数列
已知等比数列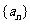 的前
的前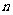 项和为
项和为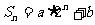 ,且
,且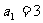 。
。
(1)
求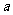 、
、 的值及数列
的值及数列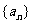 的通项公式;
的通项公式;
(2) 设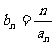 ,求数列
,求数列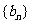 的前
的前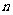 项和
项和 。
。
解:(1) 时,
时,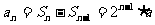 。而
。而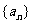 为等比数列,得
为等比数列,得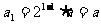 ,
,
又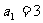 ,得
,得 ,从而
,从而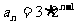 。又
。又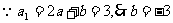 。
。
(2) ,
,
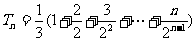

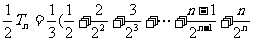
 得
得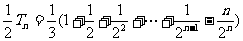 ,
,
 。
。
16.已知函数 ,当
,当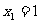 时,
时,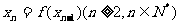 ,求数列
,求数列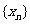 的通项公式与
的通项公式与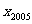 。
。
解:由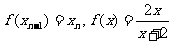 ,得
,得 ,即
,即 ,
,
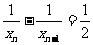 ,所以,数列
,所以,数列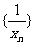 是以首项
是以首项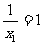 ,公差为
,公差为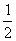 的等差数列。
的等差数列。
 ,
,  ,
,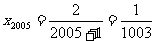 。
。
15.已知数列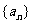 满足
满足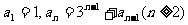 。
。
(1) 求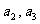 ;
;
(2) 证明: 。
。
(1) 解: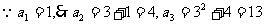 。
。
(2) 证明:由已知 ,故
,故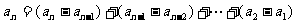
 , 所以证得
, 所以证得 。
。
14.已知函数 定义在正整数集上,且对于任意的正整数
定义在正整数集上,且对于任意的正整数 ,都有
,都有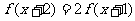
 ,且
,且 ,则
,则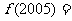 ______________。
______________。
解析:由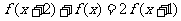 知函数
知函数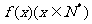 当
当 从小到大依次取值时对应的一系列函数值组成一个等差数列,
从小到大依次取值时对应的一系列函数值组成一个等差数列,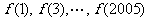 形成一个首项为
形成一个首项为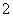 ,公差为
,公差为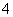 的等差数列,
的等差数列,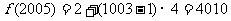 。 答案:
。 答案:
13.对于每一个正整数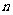 ,抛物线
,抛物线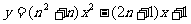 与
与 轴交于
轴交于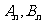 两点,则
两点,则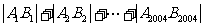 的值为______________。
的值为______________。
解析:令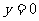 得
得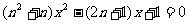 ,
,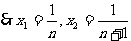 ,
,
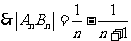
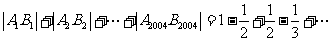
 。
答案:
。
答案: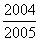
12.若数列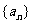 满足
满足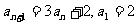 ,则通项公式
,则通项公式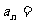 _____________.
_____________.
解析:由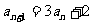 ,得
,得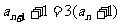 ,这表明数列
,这表明数列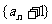 是首项为
是首项为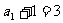 ,公比
,公比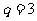 的等比数列,于是有
的等比数列,于是有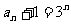 ,即
,即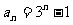 。
答案:
。
答案:
11.等差数列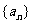 共有
共有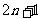 项,其中奇数项之和为
项,其中奇数项之和为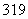 ,偶数项之和为
,偶数项之和为 ,则其中间项为______________.
,则其中间项为______________.
解析:依题意,中间项为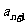 ,于是有
,于是有 解得
解得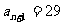 . 答案:
. 答案: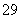
10.三个数 成等比数列,且
成等比数列,且 ,则
,则 的取值范围是 ( )
的取值范围是 ( )
(A)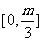 (B)
(B)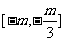 (C)
(C)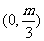 (D)
(D)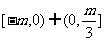
解析:设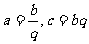 ,则有
,则有 。当
。当 时,
时, ,而
,而 ,
,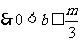 ;当
;当 时,
时,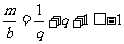 ,即
,即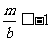 ,而
,而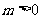
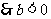 ,则
,则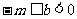 ,故
,故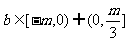 。 答案:D
。 答案:D
9.弹子跳棋共有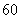 颗大小相同球形弹子,现在棋盘上将它们叠成正四面体形球垛,使剩下的弹子尽可能的少,那么剩余的弹子共有
( )
颗大小相同球形弹子,现在棋盘上将它们叠成正四面体形球垛,使剩下的弹子尽可能的少,那么剩余的弹子共有
( )
(A)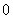 颗
(B)4颗
(C)
颗
(B)4颗
(C)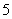 颗 (D)
颗 (D) 颗
颗
解析:最上面一层放1个,设最上一层是第一层,由上而下共有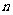 层,第
层,第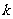 层弹子数为
层弹子数为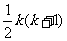 ,总弹子数为
,总弹子数为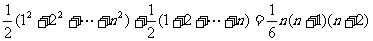 ,
,
由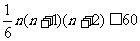 得
得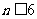 ,故
,故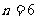 时剩余最小,且剩余
时剩余最小,且剩余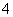 颗。 答案:B
颗。 答案:B
8.等差数列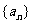 中,
中,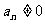 ,若
,若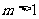 且
且 ,
,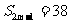 ,则
,则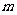 的值为
(
)
的值为
(
)
(A)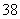 (B)
(B)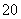 (C)
(C) 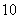 (D)
(D)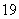
解析:由题设得 ,而
,而 ,
,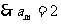 ,又
,又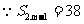 ,
,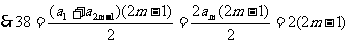 ,
,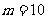 。 答案:C
。 答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com