2．已知点A(3，1)和B(-4，6)在直线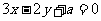的两侧，则a的取值范围(　　 )

　 (A)-7＜a＜24　　 (B)-24＜a＜7　　 (C)a＜7或a＞24　　 (D)a=7或a=24

1．　 △ABC中，三个顶点坐标A(2，4)、B(-1，2)、C(1，0)，点P(x，y)在内部及

其边界运动，则z=x-y的最大值及最小值是　　　　　　　　　　　　　　　 (　　 )

　 (A)3，1　　　　 (B)-1，-3　　　　 (C)1，-3　　　　 (D)3，-1

20．甲、乙两人独立解某一道数学题，已知该题被甲独立解出的概率为，被甲解出而乙解不出的概率为。　 (1)求该题被乙独立解出的概率；

　 (2)(文科)求恰有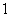人能解出这道题目的概率。(理科)求解出该题人数的期望与方差。

简解　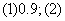 (文科)。(理科)。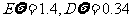

19．在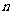个大小相同的均匀的球中，有白球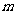个。

　(1)不放回地逐个抽取个小球，求其中恰有个白球的概率；

(2)每次抽取后又放回地逐个抽取个小球，求其中恰有个白球的概率。

(3)(理科)每次抽取后又放回地逐个抽取个小球，求其中白球个数的期望和方差。

简解 ；

　　 。

18．设掷一颗均匀的正方体玩具两次，此玩具的六个表面分别刻有数字。

(文科)求掷得的点数之和小于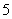的概率。(理科)设为掷得的点数差的绝对值，求。

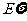简解 (文科)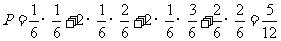。　 (理科)

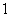
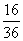
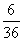
所以。

17．甲、乙两人参加一次测试，已知在备选的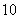道试题中，甲能答对其中的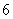道题，乙能答对其中的道题，规定每次测试都从备选题中随机抽取出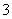题进行测试，至少答对题才算合格。

(1)(文科)分别求甲、乙两人测试合格的概率；(理科)求甲答对测试题数的概率分布及数学期望；

(2)求甲、乙两人中至少有一人考试合格的概率。

简解 (1)(文科)甲合格的概率为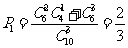，乙合格的概率为；(理科)

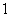
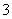
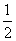
所以。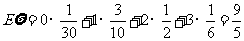

(2)两人中至少有一人合格的概率为。

16．已知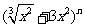展开式中各项的系数之和比各项的二项式系数之和大。

　 (1)求展开式中二项式系数最大的项；　　 (2)求展开式中系数最大的项。

简解　 由题意，，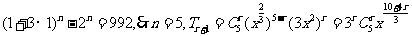

(1)展开式中二项式系数最大的项是，；

(2)由解得为所求的系数最大的项。

15．某仪器显示屏上的每个指示灯均以红色或蓝色来表示两种不同的信号，已知一排有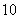个指示灯。求分别满足下列条件时，显示屏共能显示的不同的信号数的种数。

　 (1)要求每次显示其中的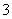个，且恰好有个相邻的同时显示；

　 (2)要求每次显示其中的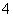个，且恰有个相邻的同时显示。

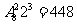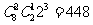简解　　 (1)或；　　 (2)。

14．已知从甲地到乙地的海底光缆有个接点，其中有一个接点发生故障，为了及时排除故障，需要尽快断定故障发生点。以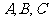三个接点为例，检查接点的方法如下：在接点处分别检查两段，若两段都有问题，则可断定点存在问题；若只有一段存在问题，则接点正常。设至少需要检查的接点数为个，则的最大值为　　　　　 。()

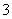13．抛掷一枚硬币若干次，每次正面向上得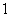分，反面向上得分。

(文科)则恰好得到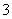分的概率为　　　 。()(理科)则恰好得到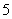分的概率为　　　 。()