
3、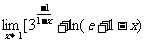 ]的值是………………………………………………( )
]的值是………………………………………………( )
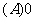
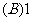
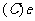
 不存在;
不存在;
2、已知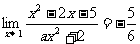 ,则常数
,则常数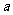 的值为…………………………………( )
的值为…………………………………( )
 (
(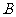 )
)
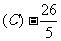
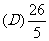 ;
;
1、下列数列极限为1的是…………………………………………………………(
)

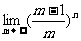 ;
;
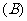
 ;
;
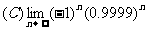 ;
;
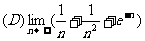 。
。
20.在棱长为a的正方体OABC--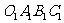 中,E、F分别是棱AB、BC上的动点,且AE=BF。
中,E、F分别是棱AB、BC上的动点,且AE=BF。
(1) 求证: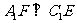 ;
;
(2) 当三棱锥B -BEF的体积取得最大值时,求二面角B
-BEF的体积取得最大值时,求二面角B -EF-B的大小。
-EF-B的大小。
19.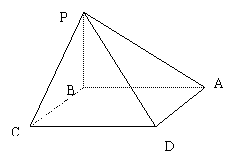 如图四棱锥P---ABCD的底面是边长为a的正方形,PB
如图四棱锥P---ABCD的底面是边长为a的正方形,PB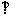 面ABCD。
面ABCD。
(1) 若面PAD与面ABCD所成的二面角为60 ,求这个四棱锥的体积;
,求这个四棱锥的体积;
(2) 证明:无论四棱锥的高怎样变化,面PAD与面PCD所成的二面角恒大于90
18.如图,正三棱柱ABC--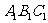 中,D是BC的中点,AB=a.
中,D是BC的中点,AB=a.
(1)  求证:
求证: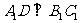
(2) 求点D到平面ACC 的距离;
的距离;
(3) 判断A B与平面ADC
B与平面ADC 的位置关系,并证明你的结论
的位置关系,并证明你的结论
17.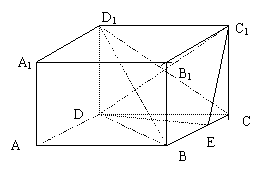 如图ABCD-
如图ABCD- 是正四棱柱,侧棱长为1,底面边长为2,E是棱BC的中点。
是正四棱柱,侧棱长为1,底面边长为2,E是棱BC的中点。
(1) 求三棱锥D -DBC的体积;
-DBC的体积;
(2) 证明BD // 平面C
// 平面C DE
DE
(3) 求面C DE与面CDE所成二面角的正切值。
DE与面CDE所成二面角的正切值。
15.已知三棱柱ABC-A B
B C
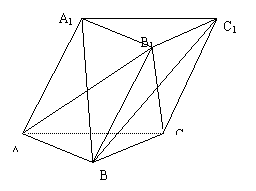
C ,如图所示中底面边长和侧棱长均为a ,侧面A
,如图所示中底面边长和侧棱长均为a ,侧面A ACC
ACC
 底面ABC,A
底面ABC,A B=
B=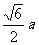 。
。
(1)  求异面直线AC与BC
求异面直线AC与BC 所成角的余弦值;
所成角的余弦值;
(2) 求证:A B
B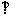 面AB
面AB C
C
|
|
|
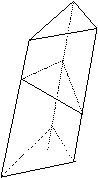 16.如图,点P为斜三棱柱ABC-A
16.如图,点P为斜三棱柱ABC-A B
B C
C 的侧棱BB
的侧棱BB 上一点,PM
上一点,PM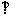 BB
BB 交AA
交AA 于点M;PN
于点M;PN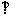 BB
BB 交CC
交CC 于点N。
于点N。
|
|
|||||
|
 |
||||
(1)
|
 MN
MN
(2) 在任意三角形DEF中有余弦定理DE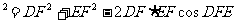 。拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角的关系式,并予以证明。
。拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角的关系式,并予以证明。
14.把半径为3cm ,中心角为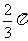 的扇形卷成一个圆锥形容器,这个容器的容积为:_________________
的扇形卷成一个圆锥形容器,这个容器的容积为:_________________
13.在正四棱锥P-ABCD中,若侧面与底面所成二面角的大小为60 ,则异面直线PA与BC所成角的大小为:_____________________ (用反三角函数值表示)
,则异面直线PA与BC所成角的大小为:_____________________ (用反三角函数值表示)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com