
4、虚拟语气中情态动词的用法
第一节 知识点概述
3、情态动词后接不定式完成体的不同意义
2、情态动词表示推测的语义差别
 高考重点要求:
高考重点要求:
1、情态动词的基本用法
48. 解答多参型问题时,关键在于恰当地引出参变量, 想方设法摆脱参变量的困绕.这当中,参变量的分离、集中、消去、代换以及反客为主等策略,似乎是解答这类问题的通性通法.
二 运算能力
每年高考都说要控制运算量,但结果是每年都控制不了.理由很简单:有数学,就有运算.
不厌其繁的运算,可以培养我们的耐性,和坚忍不拔的性格.
问题1任一分数都可以写成有限小数或无限循环小数的形式,你相信吗?试几个看看.
(1) =
;
=
;
(2) =
;
=
;
(3)请你自己写一个试试: .
 问题2已知三角形的三个顶点分别是
问题2已知三角形的三个顶点分别是 ,
,
求角平分线AM所在直线的方程.
 问题3(如图)已知正四棱锥
问题3(如图)已知正四棱锥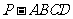 的各条棱长均为1,
的各条棱长均为1,
E,F分别为VB,VC的中点.
(I)求平面PAB与平面PBC所成的角的大小;
(II)求点A到平面PBC的距离;
(III)求直线AE与平面PBC所成的角的大小;
(IV)求异面直线AE与BF所成的角的大小;
问题4某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测
点同时听到了一声巨响,正东观测点听到的时间比其他两观测点晚4s. 已知各观测点
到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为
340m/ s :相关各点均在同一平面上)
问题5设直线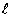 与椭圆
与椭圆 相交于A、B两点,
相交于A、B两点,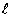 又与双曲线x2–y2=1相交于C、
又与双曲线x2–y2=1相交于C、
D两点,C、D三等分线段AB. 求直线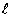 的方程.
的方程.
问题解答:问题1(略).问题2
解(一):可得 ,
,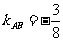 ,设直线AM的斜率为
,设直线AM的斜率为 ,则
,则
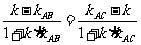 ,即
,即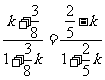 ,得
,得 ,
,
有 ,解得
,解得 ,
,
 (舍去)
(舍去)
得角平分线AM的方程为:
即 .
.
解(二): ,它的单位向量
,它的单位向量
 ,它的单位向量
,它的单位向量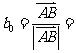

则AM与 (
(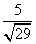 +
+ ,
,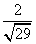
 )同向
)同向
得 ,(下同解一).
,(下同解一).
问题3解:(I)(如图)以正方形ABCD的中心为原点,建立空间直角坐标系,则
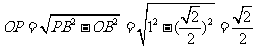
得 ,
, ,
,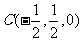 ,
,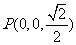
 ,
, ,
,
设平面PBC的法向量为 ,则
,则 ,
,
有 ,得
,得 ,有
,有 ,则
,则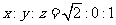
得 ,同理得平面PBC的法向量
,同理得平面PBC的法向量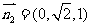 ,则
,则
 ,
,
而平面PAB与平面PBC所成的角为钝角,所以它的大小为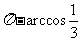 .
.
(II)由 ,设
,设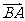 与
与 所成的角为
所成的角为 ,则
,则

则点A到平面PBC的距离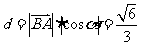 .
.
(III)可得E ,有
,有 ,设
,设 与
与 所成的角为
所成的角为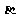 ,则
,则
 ,
,
得AE与平面PBC所成的角为 .
.
(IV)可得F ,得
,得 ,设
,设 与
与 所成的角为
所成的角为 ,则
,则

得AE与BF所成的角为 .
.
问题4 解:如图,

以接报中心为原点O,正东、正北方向为x轴、y轴正向,建立直角坐标系.设A、B、C分别是西、东、北观测点,则A(-1020,0),B(1020,0),C(0,1020)
设P(x,y)为巨响为生点,由A、C同时听到巨响声,得|PA|=|PB|,故P在AC的垂直平分线PO上,PO的方程为y=-x,因B点比A点晚4s听到爆炸声,故|PB|- |PA|=340×4=1360
由双曲线定义知P点在以A、B为焦点的双曲线 上,
上,
依题意得a=680, c=1020,

用y=-x代入上式,得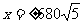 ,∵|PB|>|PA|,
,∵|PB|>|PA|,

答:巨响发生在接报中心的西偏北450距中心 处.
处.
问题5解:首先讨论l不与x轴垂直时的情况,设直线l的方程为
y=kx+b,如图所示,l与椭圆、双曲线的交点为:
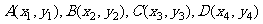

依题意有 ,由
,由
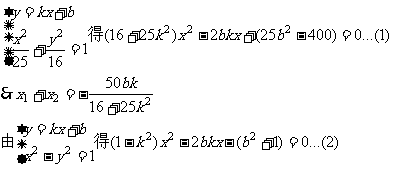
若 ,则与双曲线最多只有一个交点,不合题意,故
,则与双曲线最多只有一个交点,不合题意,故
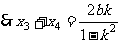
由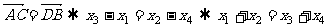

故l的方程为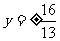
(ii)当b=0时,由(1)得

由
故l的方程为
再讨论l与x轴垂直的情况.
设直线l的方程为x=c,分别代入椭圆和双曲线方程可解得,

综上所述,故l的方程为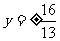 、
、 和
和
47. 解答信息型问题时,透彻理解问题中的新信息,这是准确解题的前提.
46. 解答开放型问题时,需要思维广阔全面,知识纵横联系.
45. 解答选择题的特殊方法是什么?(顺推法,估算法,特例法,特征分析法,直观选择法,逆推验证法等等)
44.只要的求导公式有哪些?
(1) ,(2)
,(2) ,(3)
,(3) ,(4)
,(4) ,(5)
,(5)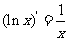 ,
,
(6) ,(7)
,(7) ,(8)
,(8) ,(9)
,(9) ,
,
(10) ,(11)
,(11) ,(12)
,(12) .
.
43. 通径是抛物线的所有焦点弦中最短的弦.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com