
10.已知函数 (a∈(0,1)),求f(x)的最值,并讨论周期性,奇偶性,单调性。
(a∈(0,1)),求f(x)的最值,并讨论周期性,奇偶性,单调性。
解:三角函数式降幂

∴ f(x)= 令
令 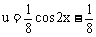
则 y=au ∴ 0<a<1 y=au是减函数
∴ 由 得
得 ,此为f(x)的减区间
,此为f(x)的减区间
由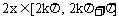 得
得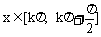 ,此为f(x)增区间
,此为f(x)增区间
∵ u(-x)=u(x) ∴ f(x)=f(-x), f(x)为偶函数
∵ u(x+π)=f(x), ∴ f(x+π)=f(x)
∴ f(x)为周期函数,最小正周期为π
当x=kπ(k∈Z)时,ymin=1
当x=kπ+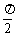 (k∈Z)时,ynax=
(k∈Z)时,ynax=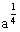
[探索题]函数f(x)=1-2a-2acosx-2sin2x的最小值为g(a),a∈R,
(1)求g(a);
(2)若g(a)=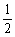 ,求a及此时f(x)的最大值.
,求a及此时f(x)的最大值.
解:(1)f(x)=1-2a-2acosx-2(1-cos2x)
=2cos2x-2acosx-1-2a
=2(cosx-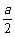 )2-
)2-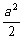 -2a-1.
-2a-1.
若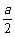 <-1,即a<-2,则当cosx=-1时,
<-1,即a<-2,则当cosx=-1时,
f(x)有最小值g(a)=2(-1-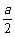 )2-
)2-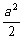 -2a-1=1;
-2a-1=1;
若-1≤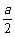 ≤1,即-2≤a≤2,则当cosx=
≤1,即-2≤a≤2,则当cosx=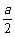 时,f(x)有最小值g(a)=-
时,f(x)有最小值g(a)=-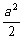 -2a-1;
-2a-1;
若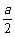 >1,即a>2,则当cosx=1时,f(x)有最小值g(a)=2(1-
>1,即a>2,则当cosx=1时,f(x)有最小值g(a)=2(1-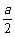 )2-
)2-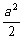 -2a-1=1-4a.
-2a-1=1-4a.
∴g(a)=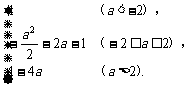
(2)若g(a)=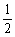 ,由所求g(a)的解析式知只能是-
,由所求g(a)的解析式知只能是-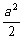 -2a-1=
-2a-1=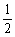 或1-4a=
或1-4a=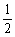 .
.
由 a=-1或a=-3(舍).
a=-1或a=-3(舍).
由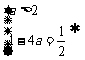 a=
a=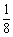 (舍).
(舍).
此时f(x)=2(cosx+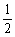 )2+
)2+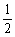 ,得f(x)max=5.
,得f(x)max=5.
∴若g(a)=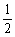 ,应a=-1,此时f(x)的最大值是5.
,应a=-1,此时f(x)的最大值是5.
备选题
9. (2006陕西)已知函数f(x)=sin(2x-)+2sin2(x-) (x∈R)
(Ⅰ)求函数f(x)的最小正周期 ; (2)求使函数f(x)取得最大值的x的集合
解:(Ⅰ) f(x)=sin(2x-)+1-cos2(x-)
= 2[sin2(x-)- cos2(x-)]+1
=2sin[2(x-)-]+1
= 2sin(2x-) +1
∴ T==π
(Ⅱ)当f(x)取最大值时, sin(2x-)=1,有 2x- =2kπ+
即x=kπ+ (k∈Z) ∴所求x的集合为{x∈R|x= kπ+ , (k∈Z)}
8.(2006
浙江)已知函数f(x)=-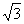 sin2x+sinxcosx.
sin2x+sinxcosx.
(Ⅰ) 求f(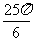 )的值;
)的值;
(Ⅱ) 设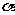 ∈(0,
∈(0,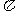 ),f(
),f(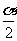 )=
)= -
-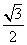 ,求sin
,求sin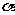 的值.
的值.
解:(Ⅰ) 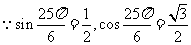
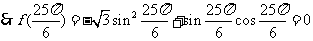
(Ⅱ) 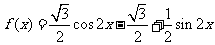

 解得
解得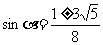

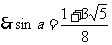
7.设 ,若方程
,若方程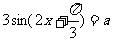 有两解,求
有两解,求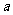 的取值范围。
的取值范围。
解:设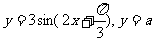 ,
,
要使两函数图象有交点,由图可知 。
。
6.4 R.
R.
[解答题]
6. 半径为R的圆的内接矩形周长的最大值等于__________.
◆练习简答:1-4:BBCC;5. 令t=sinx+cosx,则y= 最小值
最小值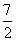
5.函数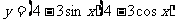 的最小值等于________。
的最小值等于________。
4.(2007 全国卷Ⅱ)函数f(x)=|sinx+cosx|的最小正周期是 ( )
A.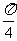 B.
B. C.π D.2π
C.π D.2π
[填空题]
3.(2006辽宁)函数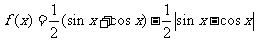 ,的值域是 ( )
,的值域是 ( )
(A) (B)
(B) 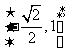 (C)
(C)  (D)
(D) 
2.(2007全国卷Ⅱ)已知函数 内是减函数,则 ( )
内是减函数,则 ( )
A.0<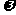 ≤1 B.-1≤
≤1 B.-1≤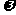 <0 C.
<0 C.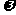 ≥1 D.
≥1 D.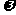 ≤-1
≤-1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com