
3、在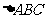 中,若
中,若 ,则
,则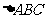 的形状为 .
的形状为 .
2、在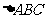 中,A>B是
中,A>B是 成立的 .条件.
成立的 .条件.
1、在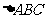 中,已知
中,已知 ,则
,则 = .
= .
(二)、关于三角形内角的常用三角恒等式:
1.三角形内角定理的变形
由A+B+C=π,知A=π-(B+C)可得出:
sinA=sin(B+C),cosA=-cos(B+C).
而 .有:
.有: ,
,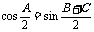 .
.
2.常用的恒等式:
(1)sinA+sinB+sinC=4cos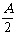 cos
cos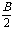 cos
cos .
.
(2)cosA+cosB+cosC=1+4sin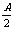 sin
sin sin
sin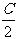 .
.
(3)sinA+sinB-sinC=4sin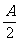 sin
sin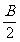 cos
cos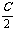 .
.
(4)cosA+cosB-cosC=-1+4cos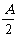 cos
cos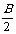 sin
sin .
.
(5)sin2A+sin2B+sin2C=4sinAsinBsinC.
(6)cos2A+cos2B+cos2C=-1-4cosAcosBcosC.
(7)sin2A+sin2B+sin2C=2+2cosAcosBcosC.
(8)cos2A+cos2B+cos2C=1-2cosAcosBcosC.
(一).三角形中的各种关系
设△ABC的三边为a、b、c,对应的三个角为A、B、C.
1.角与角关系:A+B+C = π,
2.边与边关系:a + b > c,b + c > a,c + a > b,
a-b < c,b-c < a,c-a > b.
3.边与角关系:
1)正弦定理 
2)余弦定理 c2 = a2+b2-2bccosC,b2 = a2+c2-2accosB,a2 = b2+c2-2bccosA.
它们的变形形式有:a = 2R sinA,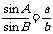 ,
, .
.
3)射影定理: a=b·cosC+c·cosB,
b=a·cosC+c·cosA,
c=a·cosB+c·cosA.
4)正切定理: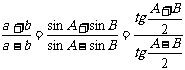
…………….(轮换)
5)模尔外得公式:

6)半角定理: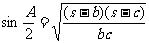
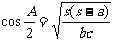
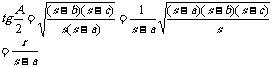
(以上公式均轮换)
7)面积公式:
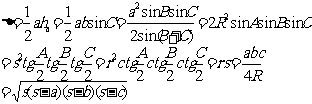
本节公式中, ,r为内切圆半径,R为外接圆半径,Δ为三角形面积.
,r为内切圆半径,R为外接圆半径,Δ为三角形面积.
8.已知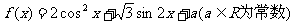
(1) 若x∈R,求f(x)的单调递增区间;
(2)
若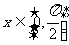 时,f(x)的最大值为4,求
时,f(x)的最大值为4,求 的值
的值
[解](1)由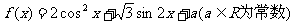

 使
使
 ,解得
,解得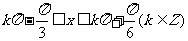 ,
,

(2)由f(x) ,因此f(x)在
,因此f(x)在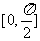 上的最大值为
上的最大值为 +3,使
+3,使 +3=4,
+3=4, 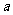 =1.
=1.
6.化简
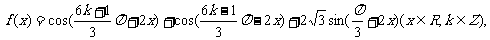
并求函数 的值域和最小正周期和递增区间.
的值域和最小正周期和递增区间.
解: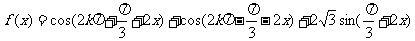
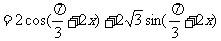
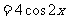
所以函数f(x)的值域为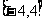 ,最小正周期
,最小正周期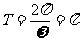
由 .(k∈Z)
.(k∈Z)
(2006上海) 求函数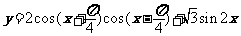 的值域和最小正周期.
的值域和最小正周期.
[解] 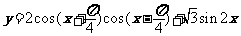
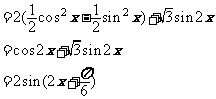
∴ 函数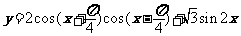 的值域是
的值域是 ,最小正周期是
,最小正周期是 ;
;
(2005重庆卷)若函数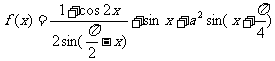 的最大值为
的最大值为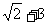 ,试确定常数a的值.
,试确定常数a的值.
解: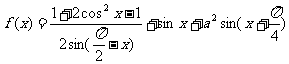


因为 的最大值为
的最大值为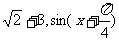 的最大值为1,则
的最大值为1,则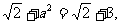
所以
19. [解](1) ,
,
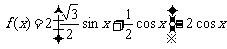

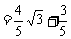 .
.
(2)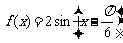 ,
,
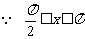 ,
, 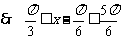 ,
, 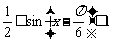 ,
,
 函数
函数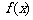 的值域为
的值域为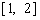 .
.
5.函数 的值域是_____________[
的值域是_____________[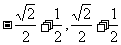 ]
]
(2006安徽)设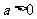 ,对于函数
,对于函数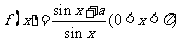 ,下列结论正确的是( )
,下列结论正确的是( )
A.有最大值而无最小值 B.有最小值而无最大值
C.有最大值且有最小值 D.既无最大值又无最小值
[例1]
试求函数y=sinx+cosx+2sinxcosx+2的最大值和最小值,若x∈[0,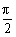 ]呢?
]呢?
剖析:注意sinx+cosx与sinx·cosx之间的关系,进行换元可将原函数转化成一元二次函数来解.
解:令t=sinx+cosx= sin(x+
sin(x+ )∈[-
)∈[- ,
, ],则y=t2+t+1∈[
],则y=t2+t+1∈[ ,3+
,3+ ],即最大值为3+
],即最大值为3+ ,最小值为
,最小值为 .当x∈[0,
.当x∈[0,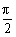 ]时,则t∈[1,
]时,则t∈[1, ],此时y的最大值是3+
],此时y的最大值是3+ ,而最小值是3.
,而最小值是3.
评述:此题考查的是换元法,转化思想,在换元时要注意变量的取值范围.
(2006广东)已知函数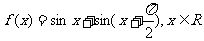
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求 的最大值和最小值;
的最大值和最小值;
(Ⅲ)若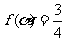 ,求
,求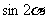 的值
的值
解: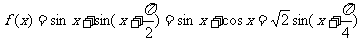
(Ⅰ) 的最小正周期为
的最小正周期为 ;
;
(Ⅱ) 的最大值为
的最大值为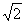 和最小值
和最小值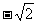 ;
;
(Ⅲ)因为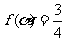 ,即
,即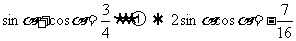 ,即
,即 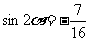
(2006春上海19) 已知函数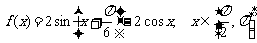 .
.
(1)若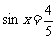 ,求函数
,求函数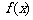 的值; (2)求函数
的值; (2)求函数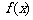 的值域.
的值域.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com