
5. 为了使y=sinωx(ω>0)在区间[0,1]上至少出现50次最大值,则ω的最小值是
4.已知sinα+cosβ=1,则y=sin2α+cosβ的取值范围是__________.
3.(2005江西)设函数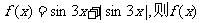 为 ( )
为 ( )
A.周期函数,最小正周期为 B.周期函数,最小正周期为
B.周期函数,最小正周期为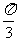
C.周期函数,数小正周期为 D.非周期函数
D.非周期函数
2.(2006全国)函数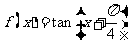 的单调增区间为 ( )
的单调增区间为 ( )
A 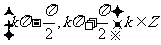 B
B 
C 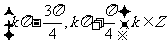 D
D 
1.(2005浙江)已知k<-4,则函数y=cos2x+k(cosx-1)的最小值是 ( )
(A) 1 (B) -1 (C) 2k+1 (D) -2k+1
3.三角函数求最值的方法: 化Asin(ωx+φ), 换元法,配方法,数形结合,不等式法,单调性法等.
2. 函数y=Asin(ωx+φ),x∈R(其中A>0,ω>0)的性质:
周期: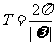 ;
;
单调递增区间:由2 kπ-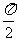 ≤ωx+φ≤2 kπ+
≤ωx+φ≤2 kπ+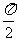 (k∈Z)可解得.
(k∈Z)可解得.
单调递减区间.由2 kπ+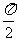 ≤ωx+φ≤2 kπ+
≤ωx+φ≤2 kπ+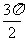 ](k∈Z)可解得.
](k∈Z)可解得.
类似可求,对称轴和对称中心.
特别提醒:若A或ω是负数,单调区间应在相反的单调区间内求。
y=Acos(ωx+φ)也类似。
1.三角函数的性质:(结合图象理解, 表中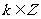 ))
))
|
|
y=sinx |
y=cosx |
y=tanx |
y=cotx |
|
定义域 |
R |
R |
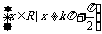 |
{x∈R|x≠kπ} |
|
值域 |
[-1,1] |
[-1,1] |
R |
R |
|
周期 |
2π |
2π |
π |
π |
|
奇偶性 |
奇函数 |
偶函数 |
奇函数 |
奇函数 |
|
增区间 |
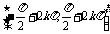 |
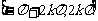 |
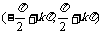 |
无 |
|
减区间 |
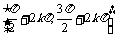 |
 |
无 |
(kπ,kπ+π) |
|
对称轴 |
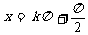 |
x=kπ |
无 |
|
|
对称 中心 |
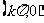 |
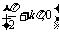 |
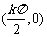 |
(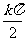 ,0) ,0) |
2.能把一般的三角函数变形为y=Asin(ωx+φ)的形式,并能求解它的周期、最值、单调区间以及奇偶性、图象的对称性等问题。
1.掌握正、余弦函数,正余切函数的性质;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com