(四)实验归纳总结：

1．力的合成要遵循平行四边形定则。两个共点力的合力随夹角的变化而变化。

夹角为0⁰(作用在同一直线上且方向相同)时：F=F₁+F₂，F的方向与F₁、F₂的方向相同。夹角为180⁰(作用在同一直线上且方向相反)时：F=|F₁-F₂|，F的方向与两个力中较大的那个力方向相同。两个共点力的合力的大小范围：大于等于二力之差，小于等于二力之和，即|F₁-F₂|≤F≤F₁+F₂。

2．两个大小一定的力F₁、F₂，当它们间的夹角由0⁰增大到180⁰的过程中，夹角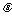越大，合力就越小；合力可能大于某一分力，也可能小于某一分力。

3．矢量和标量：

即有大小又有方向的物理量叫矢量，矢量运算遵循平行四边形定则。只有大小没有方向的物理量叫标量，标量运算遵循代数运算法则。力既有大小，又有方向，故力是矢量。

4．实验归纳法是科学研究的重要方法，要通过提出假设，设计实验，实验研究，数据分析，归纳总结，形成结论。

[例题1]大小不变的F₁、F₂两个共点力的合力为F，则有：

A．合力F一定大于任一个分力　　　　　 B．合力的大小既可等于F₁，也可等于F₂

C．合力有可能小于任一个分力　　　　　 D．合力F的大小随F₁、F₂间夹角增大而减小。

解析：正确答案是BCD

我们可以取一些特殊的数值来分析F₁、F₂的合力变化范围是|F₁－F₂|≤F≤F₁+F₂若取F₁=2N，F₂=3N则1N≤F≤5N。

当F₁与F₂夹角为180°时，合力小于分力。应排除A同时知C正确。

B对，由合力的变化范围可知正确。

D对，当F₁和F₂夹角为0°时，合力最大，当F₁，F₂夹角为180°时，合力最小，随着F₁、F₂夹角增大合力F反而减小。

说明：对于一些定性分析的选择题，有时可采用取一些特殊数值的方法来分析，这样可使分析简单、方便。

[例题2]运用平行四边形定则求互成角度的两个力的合力。

力F₁＝45N，方向水平向右。力F₂＝60N，方向竖直向上，用作图法求解合力F的大小和方向。

解：选择某一标度，利用0.5cm的长度表示15N的力，作出力的平行四边形，用刻度尺量出对角线的长度L，利用F＝15N×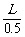即可求出。

[巩固训练]

(1)两个力互成30°角，大小分别为90N和120N，用作图法求出合力的大小和方向。

(2)两个共点力的大小都是60N，两力间的夹角为1200，求这两个力的合力？

解法一、图示法。

解法二、利用平行四边形法作出力的图示，然后利用几何知识求解。

学生讨论会得到：先求出任意两个力的合力，再求出这个合力跟第三个力的合力，直到把所有的力都合成进去，就得到其合力。因为每一次合成都遵从每两力与其合力产生共同效果的思想，所以可以这样合成。

(3)两个共点力，当它们同方向时其合力大小为7N，当它们反方向时其合力的大小为1N，问当它们互相垂直时其合力的大小是多少牛？

提示：假设F₁大于F₂，由题意可知：F₁+F₂=7，F₁-F₂=1解得：F₁=4N，F₂=3N

然后：方法一、图示法。

方法二、先利用平行四边形法则作出力的图示，再利用直角三角形知识求得合力F=5N

(4)请同学完成P₁₃的思考与讨论。

[提问]：如果两个分力F₁、F₂，他们的夹角不定，求其合力的范围。(用作图法)

同学们用作图法得到：

F_max=F₁+F₂(两力夹角为0°)

F_min=F₁－F₂(两力夹角为180°，F合于大的方向一致)

夹角在0°--180°之间，后介于　　　 F_min与F_max之间。

(三)指导学生进行分组实验

观察学生实验情况，数据处理，要求操作的规范，遵从实验结果，尽量把误差减小到最小。

要求同学用平行四边形法则作出F₁与F₂的合力，与实际合力对照，相距多远，差距大不大。

如果在实验中，对角线与合力相距比较远，那就找一找原因，是否有错误操作，即使操作完全正确，也会有实验误差，也不会完全重合。

这种情况很正常，一个规律的得出要很多人在很长时间里，进行许多此实验才总结出来，并不是一次实验就能得到。

减小误差的方法：①弹簧秤使用前要检查指针是否指在零点；②弹簧秤要与木板表面平行。

总结：可见互成角度的两个力的合成，不是简单的两个力相加减，而是用表示两个力的有向线段为邻边作平行四边形，这两邻边之间的对角线就表示合力的大小和方向。这就要平行四边形定则。以后我们还要利用这个定则进行速度、加速度等的合成，只要是矢量的合成、就遵从平行四边形定则。

(二)演示实验：互成角度的二力的合成(请两位同学上讲台帮忙)。

(1)把放木板固定在黑板上，用图钉把白纸固定在木块上。

(2)用图钉把橡皮条一端固定在A点，结点自然状态在O点，结点上系着细绳，细绳的另一端系着绳套。

(3)用两弹簧秤分别勾住绳索，互成角度地拉橡皮条，使结点到达O′点。让学生记下O′的位置，用铅笔和刻度尺在白纸上从O′点沿两条细纸的方向画线，并分别记下两只弹簧的读数F₁和F₂。

(4)放开弹簧秤，使结点重新回到O点，再用一只弹簧秤，通过细绳把橡皮条的结点拉到O′，读出弹簧秤的示数F，记下细绳的方向，按同一标度作出F₁、F₂和F的力的图示。

(5)用三角板以F₁、F₂为邻边利用刻度尺和三角尺作平行四边形，过O点画平行四边形的对角线，做出合力F的图示。

(6)改变F₁和F₂的夹角和大小，再做两次。

从实验中得出什么结论：合力F不能简单地用F₁和F₂的代数合表示。

证明：利用三角板以力F₁和F₂为邻边做平行四边形，作出其对角线F^’，看力F和F^’是否重合。

仔细观察发现，F和F^’基本重合，在误差范围内，F几乎是F₁、F₂为邻边的平行四边形的对角线。

经过前人很多次的、精细的实验，最后确认，对角线的长度、方向、跟合力的大小、方向一致，即对角线与合力重合，也就是说，对角线就表示F₁、F₂的合力。

老师归纳：求两个共点力的合力时，不是简单的将两个力相加减，而是用表示两个力的有向线段F₁和F₂为邻边作平行四边形，这两邻边之间的对角线就表示合力F的大小和方向，这就是力的平行四边形定则。

(一)探讨实验方案

先用两个力作用在物体的同一点上，使它们产生一定的作用效果，如把橡皮筋一端固定，拉加一端到某一点O，再用一个力作用于同一物体的同一点上，让它产生与第一次的两个力的作用效果相同，即也把橡皮筋拉到点O，记下各个力的大小、方向、画出力的图示，就能研究力之间的关系了。等效代替是物理中常用的一种方法。

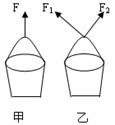
如图甲，一个人用力F可以把一桶水慢慢地提起，图乙是两个人分别用F₁、F₂两个力把同样的一桶水慢慢地提起。那么力F的作用效果与F₁、F₂的共同作用的效果如何？

学生：效果是一样的。

老师：一个力产生的效果跟几个力共同产生的效果相同，在实际问题中就可以用这个力来代替那几个力，这就是力的等效代替。这个力就叫做那几个力的合力。求几个已知力的合力的过程叫做力的合成。几个力如果都作用在物体的同一点，或者它们的作用线相交于一点，这几个力叫做共点力。我们这节课就来学习两个共点力的合成。

2．注意图示画法的规范性，在本节可以配合学生自主实验进行教学。

教学方法：实验探索法、启发式教学、归纳分析法。

教学用具：投影仪、投影片、平行四边形定则演示器、钩码、三角板、方木板、白纸、弹簧秤(两个)、橡皮条、细绳两条、刻度尺、图钉(几个)。

课时安排：1课时

教学过程

1．在讲解用作图法求解共点力合力时，可以在复习力的图示法基础上，让学生加深矢量概念的理解，同时掌握矢量的计算法则。

本课的重点是通过实验归纳出力的平行四边形法则，这同时也是本章的重点。由于学生刚开始接触矢量的运算方法，在讲解中需要从学生能够感知和理解的日常现象和规律出发，理解合力的概念，从实验现象总结出力的合成规律，由于矢量的运算法则是矢量概念的核心内容，又是学习物理学的基础，对于初上高中的学生来说，是一个大的飞跃，因此教学时，教师需要注意规范性，但是不必操之过急，通过一定数量的题目强化学生对平行四边形定则的认识。

由于力的合成与分解的基础首先是对物体进行受力分析，在前面力的知识学习中，学生已经对单个力的分析过程有了比较清晰的认识，在知识的整合过程中，教师可以通过练习做好规范演示。

关于共点力的概念讲解时需要强调不仅作用在物体的同一点的力是共点力，力的作用线相交于一点的也叫共点力。注意平行力于共点力的区分(关于平行力的合成请参考扩展资料中的“平行力的合成与分解”)，教师讲解示例中要避开这例问题。

2．通过实验探索“力的合成”所遵循的法则。

难点：“平行四边形定则”的理解。

教学建议