
9.(2009全国卷Ⅱ文)已知向量a = (2,1), a·b = 10,︱a + b ︱=  ,则︱b ︱=
,则︱b ︱=
A. B.
B.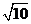 C.5
D.25
C.5
D.25
答案 C
解析
本题考查平面向量数量积运算和性质,由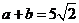 知(a+b)2=a2+b2+2ab=50,
知(a+b)2=a2+b2+2ab=50,
得|b|=5 选C.
8.(2009山东卷理)设P是△ABC所在平面内的一点,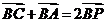 ,则( )
,则( )
A.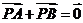 B.
B.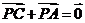 C.
C.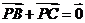 D.
D.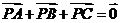
答案 B
解析 :因为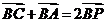 ,所以点P为线段AC的中点,所以应该选B。
,所以点P为线段AC的中点,所以应该选B。
[命题立意]:本题考查了向量的加法运算和平行四边形法则,可以借助图形解答.
7.(2009浙江卷理)设向量 ,
,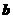 满足:
满足: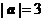 ,
,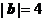 ,
, .以
.以 ,
,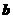 ,
, 的模为边长构成三角形,则它的边与半径为
的模为边长构成三角形,则它的边与半径为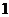 的圆的公共点个数最多为
( ) w
的圆的公共点个数最多为
( ) w
A. B.4 C.
B.4 C.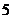 D.
D.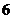
答案 C
解析 对于半径为1的圆有一个位置是正好是三角形的内切圆,此时只有三个交点,
对于圆的位置稍一右移或其他的变化,能实现4个交点的情况,但5个以上的交点不能
实现.
6.(2009广东卷理)一质点受到平面上的三个力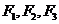 (单位:牛顿)的作用而处于平衡状态.已知
(单位:牛顿)的作用而处于平衡状态.已知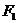 ,
,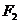 成
成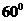 角,且
角,且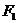 ,
,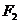 的大小分别为2和4,则
的大小分别为2和4,则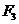 的大小为(
的大小为(  )
)  A. 6 B. 2 C.
A. 6 B. 2 C. 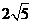 D.
D. 
答案 D
解析 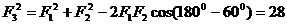 ,所以
,所以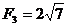 ,选D.
,选D.
5.(2009年广东卷文)已知平面向量a=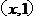 ,b=
,b= ,
则向量
,
则向量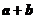 ( )
( )
A平行于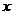 轴
B.平行于第一、三象限的角平分线
轴
B.平行于第一、三象限的角平分线
C.平行于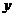 轴 D.平行于第二、四象限的角平分线
轴 D.平行于第二、四象限的角平分线
答案 C
解析 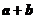
 ,由
,由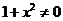 及向量的性质可知,C正确.
及向量的性质可知,C正确.
4.(2009北京卷理)已知向量a、b不共线,c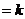 a
a b
b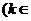 R),d
R),d a
a b,如果c
b,如果c d,那么
( )
d,那么
( )
A.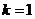 且c与d同向
B.
且c与d同向
B.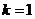 且c与d反向
且c与d反向
C.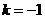 且c与d同向
D.
且c与d同向
D.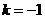 且c与d反向
且c与d反向
答案 D
解析 本题主要考查向量的共线(平行)、向量的加减法. 属于基础知识、基本运算的考
查.
取a ,b
,b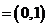 ,若
,若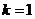 ,则c
,则c a
a b
b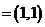 ,d
,d a
a b
b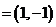 ,
,
显然,a与b不平行,排除A、B.
若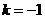 ,则c
,则c
 a
a b
b ,d
,d
 a
a b
b ,
,
即c d且c与d反向,排除C,故选D.
d且c与d反向,排除C,故选D.
2.(2009北京卷文)已知向量 ,如果
,如果
那么 ( )
A.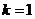 且
且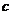 与
与 同向
B.
同向
B.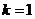 且
且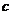 与
与 反向
反向
C.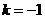 且
且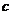 与
与 同向
D.
同向
D.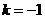 且
且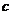 与
与 反向
反向
答案 D
.w解析 本题主要考查向量的共线(平行)、向量的加减法. 属于基础知识、基本运算考查.
∵a ,b
,b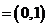 ,若
,若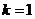 ,则c
,则c a
a b
b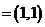 ,d
,d a
a b
b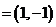 ,
,
显然,a与b不平行,排除A、B.
若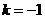 ,则c
,则c
 a
a b
b ,d
,d
 a
a b
b ,
,
即c d且c与d反向,排除C,故选D.
d且c与d反向,排除C,故选D.
1.(2009浙江卷文)已知向量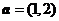 ,
, .若向量
.若向量 满足
满足 ,
, ,则
,则
 ( )
( )
A.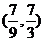 B.
B. C.
C. D.
D.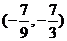
答案 D
解析 不妨设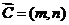 ,则
,则 ,对于
,对于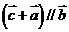 ,则有
,则有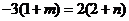 ;又
;又 ,则有
,则有 ,则有
,则有
[命题意图]此题主要考查了平面向量的坐标运算,通过平面向量的平行和垂直关系的考查,很好地体现了平面向量的坐标运算在解决具体问题中的应用.
5.变为主线、抓好训练
变是本章的主题,在三角变换考查中,角的变换,三角函数名的变换,三角函数次数的变换,三角函数式表达形式的变换等比比皆是,在训练中,强化变意识是关键,但题目不可太难,较特殊技巧的题目不做,立足课本,掌握课本中常见问题的解法,把课本中习题进行归类,并进行分析比较,寻找解题规律。
针对高考中题目看,还要强化变角训练,经常注意收集角间关系的观察分析方法.另外如何把一个含有不同名或不同角的三角函数式化为只含有一个三角函数关系式的训练也要加强,这也是高考的重点.同时应掌握三角函数与二次函数相结合的题目.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com