
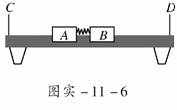
2.如图实-11-5所示是用来验证动量守恒的实验装置,弹性球1用细
线悬挂于O点,O点正下方桌子的边沿有一竖直立柱.实验时,调节
悬点,使弹性球1静止时恰与立柱上的球2接触且两球等高.将球1
拉到A点,并使之静止,同时把球2放在立柱上.释放球1,当它摆
到悬点正下方时与球2发生对心碰撞.碰后球1向左最远可摆到B点,
球2落到水平地面上的C点.测出有关数据即可验证1、2两球碰撞
时动量守恒.现已测出A点离水平桌面的距离为a.B点离水平桌面的
距离为b,C点与桌子边沿间的水平距离为c.此外:
(1)还需要测量的量是______________、________________和________________.
(2)根据测量的数据,该实验中动量守恒的表达式为________________________.(忽略小球的大小)
解析:(1)要验证动量守恒必须知道两球碰撞前后的动量变化,根据弹性球1碰撞前后的高度a和b,由机械能守恒可以求出碰撞前后的速度,故只要再测量弹性球1的质量m1,就能求出弹性球1的动量变化;根据平拋运动的规律只要测出立柱高h和桌面高H就可以求出弹性球2碰撞前后的速度变化,故只要测量弹性球2的质量和立柱高h、桌面高H就能求出弹性球2的动量变化.
(2)根据(1)的解析可以写出动量守恒的方程为
2m1=2m1+m2 .
答案:弹性球1、2的质量m1、m2
立柱高h 桌面高H
 (2)2m1=2m1+m2
(2)2m1=2m1+m2
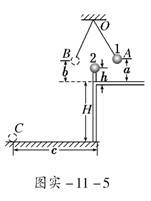
1.某同学把两块大小不同的木块用细线连接,中间夹一被压缩
了的轻质弹簧,如图实-11-4所示,将这一系统置于光滑
的水平桌面上,烧断细线,观察木块的运动情况,进行必要
的测量,验证物体间相互作用时动量守恒.
(1)该同学还必须有的器材是________________.
(2)需要直接测量的数据是___________________________
________________________________________________________________________.
(3)用所得数据验证动量守恒的关系式是_______________________________________.
解析:这个实验的思路与课本上采用的实验的原理完全相同,也是通过测平抛运动的位移来代替它们作用完毕时的速度.
答案:(1)刻度尺、天平 (2)两木块的质量m1、m2和两木块落地点分别到桌子两侧边缘的水平距离x1、x2
 (3)m1x1=m2x2
(3)m1x1=m2x2
27. (2009福建卷文)等比数列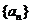 中,已知
中,已知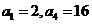


(I)求数列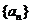 的通项公式;
的通项公式;
(Ⅱ)若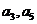 分别为等差数列
分别为等差数列 的第3项和第5项,试求数列
的第3项和第5项,试求数列 的通项公式及前
的通项公式及前 项和
项和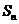 。
。
解:(I)设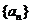 的公比为
的公比为
由已知得 ,解得
,解得
(Ⅱ)由(I)得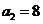 ,
, ,则
,则 ,
,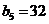
设 的公差为
的公差为 ,则有
,则有 解得
解得
从而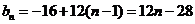
所以数列 的前
的前 项和
项和
28(2009重庆卷文)(本小题满分12分,(Ⅰ)问3分,(Ⅱ)问4分,(Ⅲ)问5分)
已知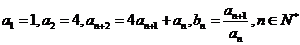 .
.
(Ⅰ)求 的值;
的值; 

(Ⅱ)设 为数列
为数列 的前
的前 项和,求证:
项和,求证: ;
;
(Ⅲ)求证: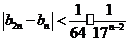 .
.
解:(Ⅰ)
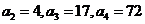 ,所以
,所以
(Ⅱ)由 得
得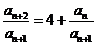 即
即
所以当 时,
时, 于是
于是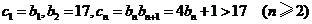
所以


(Ⅲ)当 时,结论
时,结论 成立
成立
当 时,有
时,有

所以 



26.(2009湖北卷文)已知{an}是一个公差大于0的等差数列,
且满足a3a6=55, a2+a7=16.
(Ⅰ)求数列{an}的通项公式:
(Ⅱ)若数列{an}和数列{bn}满足等式:an==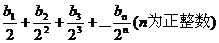 ,求数列{bn}的前n项和Sn
,求数列{bn}的前n项和Sn 

解(1)解:设等差数列 的公差为d,则依题设d>0
的公差为d,则依题设d>0 

由a2+a7=16.得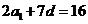 ①
①
由 得
得 ②
②
由①得 将其代入②得
将其代入②得 。即
。即



(2)令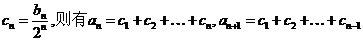
两式 相减得
相减得
于是
= -4=
-4=
25. (2009陕西卷文)已知数列 满足,
满足,
 .
.
 令
令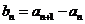 ,证明:
,证明: 是等比数列;
是等比数列;
(Ⅱ)求 的通项公式。
的通项公式。
(1)证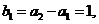
当 时,
时,
所以 是以1为首项,
是以1为首项, 为公比的等比数列。
为公比的等比数列。
(2)解由(1)知
当 时,
时,
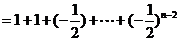



当 时,
时,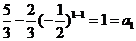 。
。
所以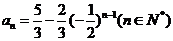 。
。
24. (2009辽宁卷文)等比数列{ }的前n 项和为
}的前n 项和为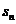 ,已知
,已知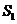 ,
, ,
, 成等差数列
成等差数列
(1)求{ }的公比q;
}的公比q;
(2)求 -
- =3,求
=3,求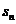


解:(Ⅰ)依题意有 

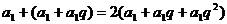
由于  ,故
,故

又 ,从而
,从而 5分
5分
(Ⅱ)由已知可得
故
从而 10分
10分
23. (2009全国卷Ⅱ理)设数列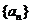 的前
的前 项和为
项和为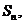 已知
已知
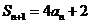
(I)设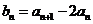 ,证明数列
,证明数列 是等比数列
是等比数列
(II)求数列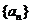 的通项公式。
的通项公式。
解:(I)由 及
及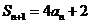 ,有
,有

由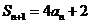 ,...①
则当
,...①
则当 时,有
时,有 .....②
.....②
②-①得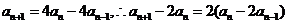
又 ,
,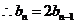
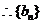 是首项
是首项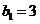 ,公比为2的等比数列.
,公比为2的等比数列.
(II)由(I)可得 ,
,
 数列
数列 是首项为
是首项为 ,公差为
,公差为 的等比数列.
的等比数列.

 ,
,
评析:第(I)问思路明确,只需利用已知条件寻找 .
.
第(II)问中由(I)易得 ,这个递推式明显是一个构造新数列的模型:
,这个递推式明显是一个构造新数列的模型: ,主要的处理手段是两边除以
,主要的处理手段是两边除以 .
.
总体来说,09年高考理科数学全国I、Ⅱ这两套试题都将数列题前置,主要考查构造新数列(全国I还考查了利用错位相减法求前n项和的方法),一改往年的将数列结合不等式放缩法问题作为押轴题的命题模式。具有让考生和一线教师重视教材和基础知识、基本方法基本技能,重视两纲的导向作用。也可看出命题人在有意识降低难度和求变的良苦用心。
22. (2009天津卷文)已知等差数列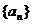 的公差d不为0,设
的公差d不为0,设

(Ⅰ)若 ,求数列
,求数列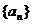 的通项公式;
的通项公式;
(Ⅱ)若 成等比数列,求q的值。
成等比数列,求q的值。
(Ⅲ)若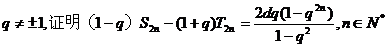
(1)解:由题设,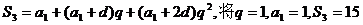
代入解得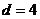 ,所以
,所以

(2)解:当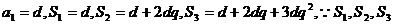 成等比数列,所以
成等比数列,所以 ,即
,即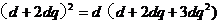 ,注意到
,注意到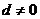 ,整理得
,整理得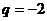
(3)证明:由题设,可得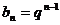 ,则
,则
 ①
①
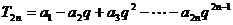 ②
②
①-②得,
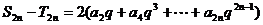
①+②得,
 ③
③
③式两边同乘以 q,得
所以
(3)证明:
=
因为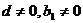 ,所以
,所以

若 ,取i=n,
,取i=n,
若 ,取i满足
,取i满足 ,且
,且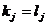 ,
,
由(1)(2)及题设知, ,且
,且



①
当 时,
时, ,由
,由 ,
,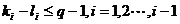
即 ,
,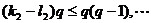

所以
因此
②
当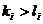 时,同理可得
时,同理可得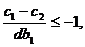 因此
因此


综上,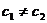
[考点定位]本小题主要考查了等差数列的通项公式,等比数列通项公式与前n项和等基本知识,考查运算能力和推理论证能力和综合分析解决问题的能力。
21.(2009江西卷文)数列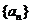 的通项
的通项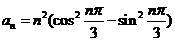 ,其前n项和为
,其前n项和为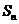 .
.
(1) 求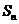 ;
;
(2)  求数列{
求数列{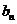 }的前n项和
}的前n项和 .
.
解: (1) 由于 ,故
,故

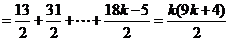 ,
,


故  (
( )
)
(2) 

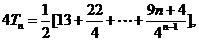
两式相减得

故 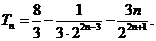
20.(2009安徽卷文)已知数列{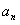 } 的前n项和
} 的前n项和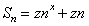 ,数列{
,数列{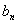 }的前n项和
}的前n项和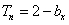
(Ⅰ)求数列{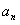 }与{
}与{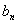 }的通项公式;
}的通项公式;
(Ⅱ)设 ,证明:当且仅当n≥3时,
,证明:当且仅当n≥3时, <
<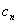


[思路]由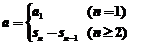 可求出
可求出 ,这是数列中求通项的常用方法之一,在求出
,这是数列中求通项的常用方法之一,在求出 后,进而得到
后,进而得到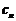 ,接下来用作差法来比较大小,这也是一常用方法。
,接下来用作差法来比较大小,这也是一常用方法。
[解析](1)由于
当 时,
时, 

又当 时
时
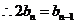
 数列
数列 项与等比数列,其首项为1,公比为
项与等比数列,其首项为1,公比为



(2)由(1)知

由 即
即 即
即
又 时
时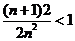 成立,即
成立,即 由于
由于 恒成立.
恒成立. 

因此,当且仅当 时,
时, 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com