
21. 甲、乙两人独立解某一道数学题,已知甲独立解出的概率为0.6,且两人中至少有一人解出的概率为0.92
(1)求该题被乙独立解出的概率;
(2)求解出该题的人数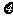 的分布列与数学期望。
的分布列与数学期望。
20. 甲、乙两个篮球队进行比赛每场比赛均不出现平局,而且若有一队胜4场,则比赛宣告结束,假设甲、乙在每场比赛中获胜的概率都是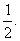
(1)求需要比赛场数ξ的分布列及数学期望Eξ;
(2)如果比赛场馆是租借的,场地租金200元,而且每赛一场追加服务费32元,那么举行一次这样的比赛,预计平均花销费用多少元钱?.
19.蓝球运动员比赛投篮,命中得1分,不中得0分,已知运动员甲投篮命中率的概率为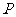 .
.
(1)
记投篮1次得分ξ,求方差 的最大值;
的最大值;
(2)
当(1)中 取最大值 时,甲一投3次篮,求所得总分
取最大值 时,甲一投3次篮,求所得总分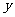 的概率分布.
的概率分布.
18. 盒中装有5节同牌号的五号电池,其中混有两节废电池,现在无放回地每次取一节电池检验,直到取到好电池为止,试回答下列问题。(1)求抽取次数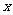 的概率分布;(2)求平均抽取多少次可取到好电池。
的概率分布;(2)求平均抽取多少次可取到好电池。
17. 甲、乙两人玩轮流抛掷一对骰子的游戏,由甲先掷,乙后掷,然后甲再掷,…. 规定先得到两颗骰子点数之和等于7的一方获胜,一旦决出胜负游戏便结束.
(1)若限定每人最多掷两次,求游戏结束时抛掷次数ξ的概率分布和数学期望;
(2)若不限定两人抛掷的次数,求甲获胜的概率.
16.. 有一批产品,其中有12件正品和4件次品,从中任取3件,若ξ表示取到次品的个数,则Dξ=
15. 若在二项式(x+1)10的展开式中任取一项,则该项的系数为奇数的概率是
14. 某工厂生产A、B、C三种不同型号的产品。产品数量之比依次为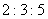 。现用分层抽样方法抽出一个容量为
。现用分层抽样方法抽出一个容量为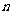 的样本,样本中A种型号产品有16件。那么此样本的容量n=
的样本,样本中A种型号产品有16件。那么此样本的容量n=
13. 若以连续掷两次骰子分别得点数m,n作为点P的横、纵坐标,则点P落在圆x2+y2=16内的概率是
12. 连掷两次骰子分别得到点数m、n,则向量(m,n)与向量(-1,1)的夹角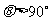 的概率是
的概率是
A. 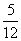 B.
B.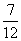 C.
C.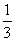 D.
D.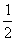
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com