
4.数形结合,数形转化是本课的重要的思想方法。
同步练习 4.4 三角函数的图象 解析式
[选择题]
3.深刻理解图象变换与函数式变换(参数变化)的关系,掌握由图象求解析式的方法。
2.正、余弦、正切函数图象的画法、变换及对称性;
思想方法:
知识总结:
1.三角函数线及运用;
2.利用相邻两零点间的距离是半个周期求ω,利用第一个零点求φ .
2.三角函数与向量的综合题是一个新的命题方向。
 [研讨.欣赏]已知电流I与时间t的关系式为
[研讨.欣赏]已知电流I与时间t的关系式为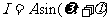 .
.
(1)右图是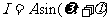 (ω>0,
(ω>0, )
)
在一个周期内的图象,根据图中数据求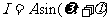
的解析式;
(2)如果t在任意一段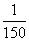 秒的时间内,电流
秒的时间内,电流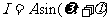 都能取得最大值和最小值,那么ω的最小正整数值是多少?
都能取得最大值和最小值,那么ω的最小正整数值是多少?
解:(1)由图可知 A=300.
设t1=-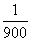 ,t2=
,t2=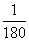 ,
,
则周期T=2(t2-t1)=2(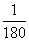 +
+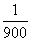 )=
)=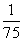 .
.
∴ ω=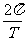 =150π.
=150π.
又当t=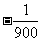 时,I=0,即sin(150π·
时,I=0,即sin(150π·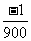 +
+ )=0,
)=0,
150π·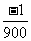 +
+ =0 ∴
=0 ∴  =
=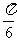 .
.
故所求的解析式为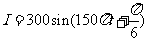 .
.
(2)依题意,周期T≤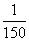 ,即
,即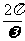 ≤
≤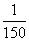 ,(ω>0)
,(ω>0)
∴ ω≥300π>942,又ω∈N*,
故最小正整数ω=943.
提炼方法:1.关键是将图形语言转化为符号语言.
2.画图:关键是确定“五点”对应的x值;不是整齐的“五点”间的一段时,要再描出端点。
 [例4](2006浙江)如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤
[例4](2006浙江)如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤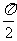 )的图象与y轴交于点(0,1).
)的图象与y轴交于点(0,1).
(Ⅰ)求φ的值;
(Ⅱ)设P是图象上的最高点,M、N是图象与x轴的交点,求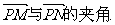
解:(I)因为函数图像过点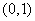 ,
,
所以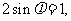 即
即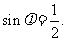
因为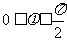 ,所以
,所以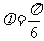 .
.
(II)由函数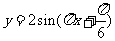 及其图像,得
及其图像,得

所以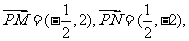 从而
从而
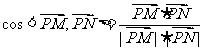
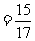 ,
,
故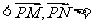
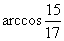 .
.
题型方法:1.利用图象所给信息求解析式;
[例1]解三角不等式组
(1)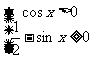 (2)
(2)
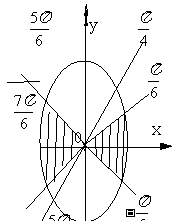 解:(1)如图:
解:(1)如图: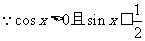
∴解集为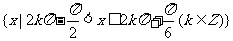
(2)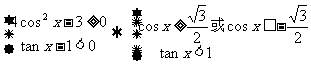
由图得解集为: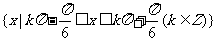
温馨提示: 利用三角函数线或单调性求解,先求出一个周期上的解再写出全部。
[例2](2006重庆)设函数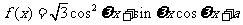 (其中
(其中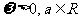 ),且
),且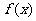 的图象在
的图象在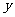 轴右侧的第一个最高点的横坐标为
轴右侧的第一个最高点的横坐标为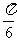 。
。
(Ⅰ)求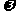 的值;
的值;
(Ⅱ)如果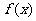 在区间
在区间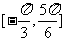 上的最小值为
上的最小值为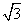 ,求
,求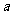 的值。
的值。

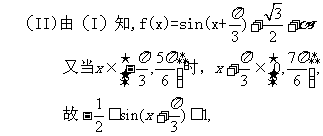

提炼方法:1.先化简,再由图象求解析式--利用第一个最大值点求ω;
2.借助三角函数线,或三角函数图象求取值范围.
[例3](2005全国卷Ⅰ)设函数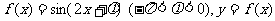 图像的一条对称轴是直线
图像的一条对称轴是直线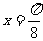 。
。
(Ⅰ)求φ; (Ⅱ)求函数y=f(x)的单调增区间;
(Ⅲ)画出函数y=f(x)在区间[0,π]上的图像。
解:(Ⅰ) 的图像的对称轴,
的图像的对称轴,
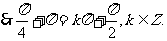
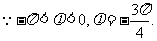
(Ⅱ)由(Ⅰ)知
由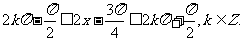
得 
∴函数y=f(x)的的单调区间为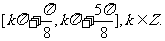
(Ⅲ)由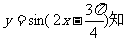
|
x |
0 |
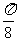 |
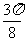 |
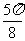 |
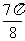 |
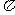 |
|
y |
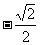 |
-1 |
0 |
1 |
0 |
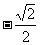 |
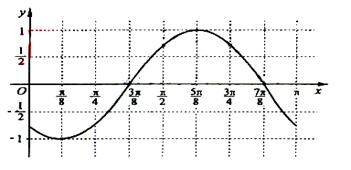 故函数
故函数
题型方法:1.求单调区间--把复合角放到单调区间内,解x的范围;
6.(i)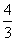 ; (ii)画图知:在一个周期上面积为
; (ii)画图知:在一个周期上面积为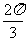 ,[
,[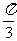 ,
,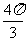 ]是1.5个周期,面积为
]是1.5个周期,面积为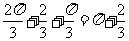 .
.
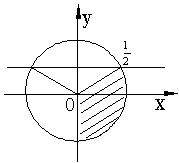
5.平移后的图象所对应的解析式为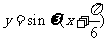 ,由图象知,
,由图象知,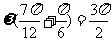 ,所以
,所以 ,答案
,答案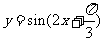 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com