
5.下列命题中,正确的是( )
A.
若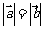 ,则
,则 B. 若
B. 若 ,则
,则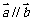 C. 若
C. 若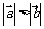 ,则
,则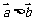 D. 若
D. 若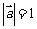 ,则
,则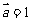
4.(04年浙江卷.文4)已知向量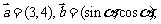 且
且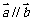 ,则
,则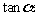 =( ).
=( ).
A.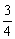 B.
B. 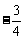 C.
C. 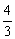 D.
D. 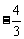
3.已知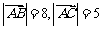 ,则
,则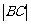 的取值范围是
(
)
的取值范围是
(
)
A. [3,8] B. (3,8) C. [3,13] D. (3,13)
2.在平行四边形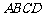 中,若
中,若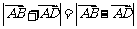 ,则必有
(
)
,则必有
(
)
A. 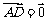 B.
B. 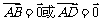 C.
C. 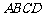 是矩形 D.
是矩形 D. 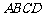 是正方形
是正方形
1.下面给出四个命题:①对于实数m和向量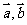 ,恒有
,恒有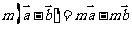
②对于实数m、n和向量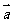 ,恒有
,恒有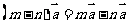
③若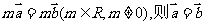
④若 ,则m=n 其中正确的命题个数是 ( )
,则m=n 其中正确的命题个数是 ( )
A、1 B、2 C、3 D、4
10.(05重庆卷)在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖。某顾客从此10张券中任抽2张,求:
(1) 该顾客中奖的概率;
(2) 该顾客获得的奖品总价值x (元)的概率分布列和期望Ex。
9.(2004年春季安徽)已知盒中有10个灯泡,其中8个正品,2个次品.需要从中取出2个正品,每次取出1个,取出后不放回,直到取出2个正品为止.设ξ为取出的次数,求ξ的分布列及Eξ.
8.一袋中装有5只球,编号为1,2,3,4,5,在袋中同时取3只,以ξ表示取出的3只球中的最大号,写出随机变量ξ的分布列.
7.金工车间有10台同类型的机床,每台机床配备的电动机功率为10 kW,已知每台机床工作时,平均每小时实际开动12 min,且开动与否是相互独立的.现因当地电力供应紧张,供电部门只提供50 kW的电力,这10台机床能够正常工作的概率为多大?在一个工作班的8 h内,不能正常工作的时间大约是多少?
6.(2003年高考·新课程)A、B两个代表队进行乒乓球对抗赛,每队三名队员,A队队员是A1、A2、A3,B队队员是B1、B2、B3,按以往多次比赛的统计,对阵队员之间胜负概率如下:
|
对阵队员 |
A队队员胜的概率 |
A队队员负的概率 |
|
A1对B1 |
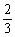 |
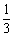 |
|
A2对B2 |
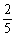 |
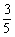 |
|
A3对B3 |
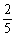 |
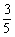 |
现按表中对阵方式出场,每场胜队得1分,负队得0分.设A队、B队最后所得总分分别为ξ、η.
(1)求ξ、η的概率分布;
(2)求Eξ、Eη.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com