
(二)进行新课:
(让学生填写下面的知识提纲)
1.功:一个物体受到__的作用,如果在力的方向上发生一段_____,这个力就对物体做了功.
做功的两个不可缺少的因素:___和在力的方向上发生的_____.
功的公式:
功的单位:_____,符号是___.功是___(矢、标)量.
2.正功和负功:
根据W=Fscosα可知:
(1)当α=________时,W=0.即当力F和位移s_____时,力F对物体不做功.这种情况,物体在力F的方向上没有发生位移.
(2)当___≤α<________时,W>0.即当力F跟位移s的夹角为___(锐、钝)角时,力F对物体做正功,这时力F是___(动、阻)力,所以,___(动、阻)力对物体做正功.
(3)当________<α≤___时,W<0.即当力F跟位移s的夹角为___(锐、钝)角时,力F对物体做负功,这时力F是___(动、阻)力,所以,___(动、阻)力对物体做负功.一个力对物体做负功,又常说成物体_____这个力做功(取绝对值).
(一)引入新课
上节课我们学习了功的概念,对功有了初步的理解,这节课我们通过习题课,进一步理解功的概念,并学会关于功的一般计算方法。
投影仪,计算机,大屏幕
讲授、讨论、练习。
2.培养学生运用所学知识分析解决实际问题的能力是本节的难点。
1.进一步理解功的概念,掌握关于功的一般计算方法是本节的重点。
2.培养学生运用所学知识分析解决实际问题的能力。
1.进一步理解功的概念,掌握关于功的一般计算方法。
10.如图为某三角函数图象的一段
(1)用正弦函数写出其中一个解析式;
(2)求与这个函数关于直线 对
对
称的函数解析式,并作出它一个周期内简图。
思路分析:由 ,由最值定A,由特殊值定
,由最值定A,由特殊值定 ,用五点法作简图。
,用五点法作简图。
解:(1)
 由图它过
由图它过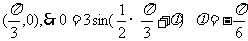 (为其中一个值)
(为其中一个值)

(2) 上任意一点,该点关于直线
上任意一点,该点关于直线 对称点为
对称点为
 关于直线
关于直线 对称的函数解析式是
对称的函数解析式是
列表:
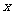 |
 |
 |
 |
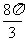 |
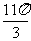 |
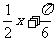 |
0 |
 |
 |
 |
 |
 |
0 |
-3 |
0 |
3 |
0 |
作图:
[探索题](2005全国Ⅰ)设函数 图像的一条对称轴是直线
图像的一条对称轴是直线 。
。
(Ⅰ)求 ;
;
(Ⅱ)求函数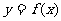 的单调增区间;
的单调增区间;
(Ⅲ)证明直线 与函数
与函数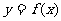 的图像不相切。
的图像不相切。
解:(Ⅰ) 的图像的对称轴,
的图像的对称轴,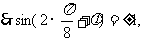


(Ⅱ)由(Ⅰ)知
由题意得

所以函数
(Ⅲ)证明:∵ 
所以曲线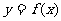 的切线斜率的取值范围为[-2,2],
的切线斜率的取值范围为[-2,2],
而直线 的斜率为
的斜率为 ,
,
所以直线 于函数
于函数 的图像不相切
的图像不相切
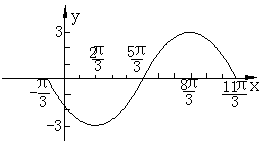
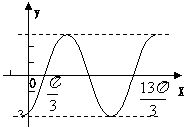
9. (2003季上海)已知函数f(x)=Asin(ωx+φ),
x∈R(其中A>0,ω>0)在一个周期内的图象如图
所示。求直线y=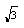 与函数f(x)图象的所有交点
与函数f(x)图象的所有交点
的坐标
[解]根据图象得A=2,T= -
-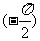 =4π,ω=
=4π,ω=
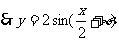 ,又由图象可得相位移为
,又由图象可得相位移为 ,
,
 .即
.即 ,
,
根据条件: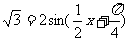 ,
,

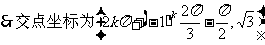
[思维点拨]按图可求得f(x)=Asin(ωx+φ),再求交点即可。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com