8．(2008年陕西卷)关于平面向量a，b，c，有下列三个命题：

①若a·b＝a·c，则b＝c.

②若a＝(1，k)，b＝(－2,6)，a∥b，则k＝－3.

③非零向量a和b满足|a|＝|b|＝|a－b|，则a与a+b的夹角为60°.

其中真命题的序号为________(写出所有真命题的序号)．

[解析]　命题①明显错误．由两向量平行的充要条件得1×6+2k＝0，k＝－3，故命题②正确．由|a|＝|b|＝|a－b|，

再结合平行四边形法则可得a与a+b的夹角为30°，命题③错误．

[答案]　②

7．在长江南岸渡口处，江水以12.5 km/h的速度向东流，渡船的速度为25 km/h.渡船要垂直地渡过长江，则航向为________．

[解析]　如图，渡船速度为，水流速度为，船实际垂直过江的速度为，依题意知，|O|＝12.5，|O|＝25，由于四边形OADB为平行四边形，则|B|＝|O|，又OD⊥BD，

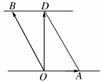
∴在Rt△OBD中，∠BOD＝30°，∴航向为北偏西30°.

[答案]　北偏西30°

6．已知非零向量，和满足·＝0，且＝，则△ABC为

(　)

A．等边三角形　 　　　　　　　　　　　 B．等腰非直角三角形

C．非等腰三角形　 　　　　　　　　　 D．等腰直角三角形

[解析]　由于+表示的向量所在直线，是∠BAC的平分线，故·＝0说明∠BAC的平分线与BC垂直，故说明三角形ABC为等腰三角形，

又＝cos∠ACB＝⇒∠ACB＝，故三角形为等腰直角三角形．

[答案]　D

5．已知||＝1，||＝，·＝0，点C在∠AOB内，且∠AOC＝30°.设＝m+nOB(m，n∈R)，则等于

(　)

A.　 　　　　　　　　　　　　　　　　　　　　 B．3

C.　 　　　　　　　　　　　　　　　　　　　 D.

[解析]　解法1：　如图建立直角坐标系：

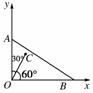
＝m(0,1)+n(，0)＝(n，m)

∴＝tg60°＝，∴＝3.

解法2：　∵cos∠COB＝cos∠60°，

∴＝，

∴＝⇒＝⇒＝，

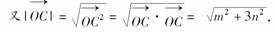
∴＝⇒＝9，∴＝3.

[答案]　B

4．已知向量a＝(1,2)，b＝(－2，－4)，|c|＝，若(a+b)·c＝，则a与c的夹角为

(　)

A．30°或150°　 　　　　　　　　　　　　 B．60°或120°

C．120°　 　　　　　　　　　　　　　　　　 D．150°

[解析]　向量a与向量a+b的夹角为π，可设向量a+b与向量c的夹角为α，则(a+b)·c＝|a+b|·|c|·cos α＝5cos α＝，所以cos α＝，α＝60°，则向量a与向量c所夹的角应为120°.答案为C.

[答案]　C

3．已知向量＝(2,2)，＝(cos α，sin α)，则向量的模的最大值是

(　)

A．3　 　　　　　　　　　　　　　　　　　　　 B．3

C.　 　　　　　　　　　　　　　　　　　　　 D．18

[解析]　由已知易得：＝+＝(2+cos α，2+sin α)，故|O|²＝(2+cos α)²+(2+sin α)²＝10+8sin≤18，即|O|≤3，故选B.

[答案]　B

2．(2009年重庆卷)已知|a|＝1，|b|＝6，a·(b－a)＝2，则向量a与b的夹角是

(　)

A.　 　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　 D.

[解析]　∵a·(b－a)＝a·b－a²＝2，∴a·b＝2+a²＝3.

∴cos<·>＝＝＝，∴a与b的夹角为.

[答案]　C

1．已知下列各式：①|a|²＝a²；②＝；③(a·b)²＝a²·b²；④(a－b)²＝a²－2a·b+b²，其中正确的有

(　)

A．1个　　　　　　 B．2个

C．3个　 　　　　　　　　　　　　　　　　　 D．4个

[解析]　①④正确．

[答案]　B