
1 若cosx=0,则角x等于( )
若cosx=0,则角x等于( )
A.kπ,(k∈Z)
B. +kπ,(k∈Z)
+kπ,(k∈Z)
C. +2kπ,(k∈Z) D.-
+2kπ,(k∈Z) D.- +2kπ,(k∈Z)
+2kπ,(k∈Z)
2 若tanx=0,则角x等于( )
若tanx=0,则角x等于( )
A.kπ,(k∈Z)
B. +kπ,(k∈Z)
+kπ,(k∈Z)
C. +2kπ,(k∈Z) D.-
+2kπ,(k∈Z) D.- +2kπ,(k∈Z)
+2kπ,(k∈Z)
3 已知cosx=-
已知cosx=- ,π<x<2π,则x等于( )
,π<x<2π,则x等于( )
A. B.
B. C.
C. D.
D.
4 若tan(3π-x)=-
若tan(3π-x)=- ,则x=
,则x=

5 满足tanx=
满足tanx= 的x的集合为
的x的集合为 
6 在闭区间[0,2π]上,适合关系式cosx=-0.4099的角有 个,用0.4099的反余弦表示的x值是
___________;用-0
在闭区间[0,2π]上,适合关系式cosx=-0.4099的角有 个,用0.4099的反余弦表示的x值是
___________;用-0 4099的反余弦表示的x的值是
_________
4099的反余弦表示的x的值是
_________
例1
(1)已知 ,求x(精确到
,求x(精确到 )
)
解:在区间 上
上 是增函数,符合条件的角是唯一的
是增函数,符合条件的角是唯一的

(2)已知 且
且 ,求x的取值集合
,求x的取值集合
解:
 所求的x的集合是
所求的x的集合是 (即
(即 )
)
(3)已知 ,求x的取值集合
,求x的取值集合
解:由上题可知: ,
,
合并为
例2已知 ,根据所给范围求
,根据所给范围求 :
:
1° 为锐角 2°
为锐角 2° 为某三角形内角 3°
为某三角形内角 3° 为第二象限角 4°
为第二象限角 4°
解:1°由题设
2°设 ,或
,或
3°
4°由题设
例3 求适合下列关系的x的集合
1° 2°
2° 3°
3°
解:1°
 所求集合为
所求集合为
2° 所求集合为
所求集合为
3°
例4 直角 锐角A,B满足:
锐角A,B满足:
解:由已知:
 为锐角,
为锐角,

例5 1°用反三角函数表示 中的角x
中的角x
2°用反三角函数表示 中的角x
中的角x
解:1° ∵ ∴
∴
又由 得
得
∴ ∴
∴
2° ∵ ∴
∴
又由 得
得
∴ ∴
∴
例6已知 ,求角x的集合
,求角x的集合
解:∵ ∴
∴
由 得
得 
由 得
得 
故角x的集合为
例7求 的值
的值
解:arctan2 = a, arctan3 = b 则tana = 2, tanb = 3
且 ,
, 
∴
而 ∴a + b =
∴a + b = 
又arctan1
=  ∴
∴ = p
= p
例8求y = arccos(sinx), ( )的值域
)的值域
解:设u = sin x ∵ ∴
∴
∴ ∴所求函数的值域为
∴所求函数的值域为
反正切函数

1°在整个定义域上无反函数
2°在 上
上 的反函数称作反正切函数,
的反函数称作反正切函数,
记作 (奇函数)
(奇函数)
2.已知三角函数求角:
求角的多值性法则:1、先决定角的象限 2、如果函数值是正值,则先求出对应的锐角x; 如果函数值是负值,则先求出与其绝对值对应的锐角x,3、由诱导公式,求出符合条件的其它象限的角
2、如果函数值是正值,则先求出对应的锐角x; 如果函数值是负值,则先求出与其绝对值对应的锐角x,3、由诱导公式,求出符合条件的其它象限的角
1.反正弦,反余弦函数的意义:
 由
由
1°在R上无反函数
2°在 上,
上, x与y是一一对应的,且区间
x与y是一一对应的,且区间 比较简单
比较简单
 在
在 上,
上, 的反函数称作反正弦函数,
的反函数称作反正弦函数,
记作 ,(奇函数)
,(奇函数)
 同理,由
同理,由
在 上,
上, 的反函数称作反余弦函数,
的反函数称作反余弦函数,
记作
|
16.(本小题13分) (1) 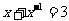   (2)解析:设F(x)=f(x)-2,即F(x)=alog2x+blog3x, 则F()=alog2+blog3=-(alog2x+blog3x)=-F(x), ∴F(2010)=-F()=-[f()-2]=-2, 即f(2010)-2=-2,故f(2010)=0 |
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效!
|
17.(本小题13分) A={x|-1<x≤5}. (1) 当m=3时,B={x|-1<x<3}, 则∁RB={x|x≤-1或x≥3}, ∴A∩(∁RB)={x|3≤x≤5}. (2)∵A={x|-1<x≤5},A∩B={x|-1<x<4}, ∴有-42+2×4+m=0,解得m=8, 此时B={x|-2<x<4},符合题意. |
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效
|
18.(本小题13分) (1)证明:∵f(x+2)=-f(x), ∴f(x+4)=-f(x+2)=-[-f(x)]=f(x), ∴f(x)是以4为周期的周期函数. (2)当0≤x≤1时,f(x)=x, 设-1≤x≤0,则0≤-x≤1, ∴f(-x)=(-x)=-x.∵f(x)是奇函数, ∴f(-x)=-f(x),∴-f(x)=-x, 即f(x)=x.故f(x)=x(-1≤x≤1) 又设1<x<3,则-1<x-2<1, ∴f(x-2)=(x-2), 又∵f(x-2)=-f(2-x)=-f[(-x)+2] =-[-f(-x)]=-f(x), ∴-f(x)=(x-2), ∴f(x)=-(x-2)(1<x<3). ∴f(x)= 由f(x)=-,解得x=-1.∵f(x)是以4为周期的周期函数.故f(x)=-的所有x=4n-1(n∈Z).令0≤4n-1≤2010,则≤n≤502,又∵n∈Z,∴1≤n≤502(n∈Z),∴在[0,2010]上共有502个x使f(x)=-. |
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效!
|
19.(本小题13分) (1)由已知得,函数的定义域为  , ,关于原点对称;  故 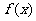 是偶函数。 是偶函数。(2)当  时,在定义域 时,在定义域 内,函数 内,函数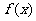 与函数 与函数 的单调性一致; 的单调性一致; , ,易得,  分别在区间 分别在区间 内为单调递减。 内为单调递减。所以,函数 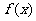 区间 区间 内为单调递减; 内为单调递减;(3)由已知得  ,由(2)可知,函数 ,由(2)可知,函数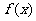 在 在 内单调递减,所以有 内单调递减,所以有 即 即 即   xsc解之得  (负值舍去) (负值舍去) |
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效!
|
20.(本小题14分) (1)当甲的用水量不超过6吨时,即  时,乙的用水量也不会超过6吨,此时 时,乙的用水量也不会超过6吨,此时 ; ;当甲的用水量超过6吨而乙的用水量没有超过6吨时,即  时,此时 时,此时  当甲乙的用水量都超过6吨时,即  时, 时,此时  综上可知,  (2)若  (舍去) (舍去)若  (符合题意) (符合题意)若  (舍去) (舍去)综上可知,甲的用水量为  (吨) (吨)付费  (元) (元)乙的用水量为  (吨) (吨)付费  (元) (元)答:略。 |

 请在各题规定的黑色矩形区域内答题,超出该区域的答案无效!
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效!
|
21.(本小题7+7=14分) (1) 法一:特殊点法 在直线  上任取两点(2、1)和(3、3),……1分 上任取两点(2、1)和(3、3),……1分则  · ·  即得点 即得点 …3 分 …3 分  即得点 即得点 将  和 和 分别代入 分别代入 上得 上得 则矩阵  则 则 法二:通法 设  为直线 为直线 上任意一点其在M的作用下变为 上任意一点其在M的作用下变为 则   代入  得: 得: 其与  完全一样得 完全一样得 则矩阵  则 则 (2) 解:(Ⅰ)消去参数  ,得直线 ,得直线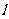 的普通方程为 的普通方程为 …3分 …3分 ,即 ,即 , ,两边同乘以  得 得 , ,得⊙  的直角坐标方程为 的直角坐标方程为 ………5分 ………5分(Ⅱ)圆心  到直线 到直线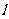 的距离 的距离 ,所以直线 ,所以直线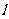 和⊙ 和⊙ 相交…7分 相交…7分(3).解:由  ,且 ,且 , ,得  ……3分 ……3分又因为  ,则有2 ,则有2 ………5分 ………5分解不等式  ,得 ,得 …………………… 7分 …………………… 7分 |
21、本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分。
(1)(本小题满分7分) 选修4-2:矩阵与变换
已知 ,若
,若 所对应的变换
所对应的变换 把直线
把直线 变换为自身,求实数
变换为自身,求实数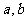 ,并求
,并求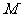 的逆矩阵。
的逆矩阵。
(2)(本题满分7分)选修4-4:坐标系与参数方程
已知直线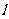 的参数方程:
的参数方程: (
( 为参数)和圆
为参数)和圆 的极坐标方程:
的极坐标方程: 。
。
①将直线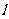 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
②判断直线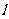 和圆
和圆 的位置关系。
的位置关系。
(3)(本题满分7分)选修4-5:不等式选讲
已知函数 . 若不等式
. 若不等式
 恒成立,求实数
恒成立,求实数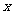 的范围。
的范围。


 惠安高级中学2011届高三数学(理)第一次单元考答题卡
惠安高级中学2011届高三数学(理)第一次单元考答题卡
(试卷满分:150分 考试时间:120分钟)
命题: 审核: 时间:2010.9
|
11.  12. 12.  13.  14. 14.  (注:最好是写成 (注:最好是写成 ) )15. ②③④ |
20、我县为提倡节约用水,居民自来水收费标准如下:每户每月用水不超过6吨时,每吨为2元,当用水超过6吨时,超过部分每吨3元,某月甲、乙两户共交水费 元,已知甲、乙两户用水分别为
元,已知甲、乙两户用水分别为 和
和 (吨)。
(吨)。
(1)求 关于
关于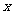 的函数;
的函数;
(2)若甲、乙两户该月共交水费26.5元,分别求出甲、乙两户该月的用水量和水费。
19、已知函数 ,(其中
,(其中 )。
)。
(1)判断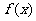 的奇偶性;
的奇偶性;
(2)若 ,判断
,判断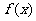 的单调性;
的单调性;
(3)当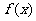 的定义域区间为
的定义域区间为 时,
时,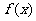 的值域为
的值域为 ,求
,求 的值。
的值。
18、已知函数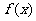 的定义域为
的定义域为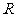 ,且满足
,且满足 。
。
(1)求证: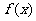 是周期函数;
是周期函数;
(2)若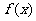 为奇函数,且当
为奇函数,且当 时,
时, ,求使
,求使 在[0,2010]上的所有
在[0,2010]上的所有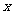 的个数。
的个数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com