
28.如图11,在梯形ABCD中,AB∥CD,AB=7,CD=1,AD=BC=5.点M、N分别在边AD、BC上运动,并保持MN∥AB,ME⊥AB,NF⊥AB,垂足分别为E、F.
(1)求梯形ABCD的面积;
(2)求四边形MEFN面积的最大值.
(3)试判断四边形MEFN能否为正方形,若能,求出
正方形MEFN的面积;若不能,请说明理由.
[命题意图]梯形的性质和图形的运动结合
[参考答案](1)分别过D,C两点作DG⊥AB于点G,CH⊥AB于点H. ∵ AB∥CD,
 ∴ DG=CH,DG∥CH. ∴ 四边形DGHC为矩形,GH=CD=1.
∴ DG=CH,DG∥CH. ∴ 四边形DGHC为矩形,GH=CD=1.
∵ DG=CH,AD=BC,∠AGD=∠BHC=90°,
∴ △AGD≌△BHC. ∴ AG=BH= =3.
=3.
∵ 在Rt△AGD中,AG=3,AD=5, ∴ DG=4.
∴  .
(3分)
.
(3分)
(2)∵ MN∥AB,ME⊥AB,NF⊥AB,
∴ ME=NF,ME∥NF. ∴ 四边形MEFN为矩形.
∵ AB∥CD,AD=BC, ∴ ∠A=∠B.
∵ ME=NF,∠MEA=∠NFB=90°,
∴ △MEA≌△NFB. ∴ AE=BF.
设AE=x,则EF=7-2x. ∵ ∠A=∠A,∠MEA=∠DGA=90°,
∴ △MEA∽△DGA. ∴ 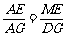 . ∴ ME=
. ∴ ME= .
(5分)
.
(5分)
∴ 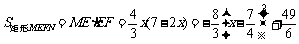 . 当x=
. 当x= 时,ME=
时,ME= <4,
<4,
∴四边形MEFN面积的最大值为 .
(7分)
.
(7分)
(3)能.由(2)可知,设AE=x,则EF=7-2x,ME= . 若四边形MEFN为正方形,
. 若四边形MEFN为正方形,
则ME=EF. 即 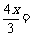 7-2x.解,得
7-2x.解,得 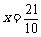 ∴ EF=
∴ EF=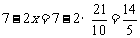 <4.
<4.
∴ 四边形MEFN能为正方形,其面积为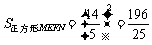 . (12分)
. (12分)
[试题来源]中考指南全真模拟试题
27. 如图,已知直线l:y=kx+2,k<0 ,与y轴交于点A,与x轴交于点B,以OA为直径的⊙P交l于另一点D,把弧AD沿直线l翻转后与OA交于点E。
(1)当k=-2时,求OE的长(4)分
(2)是否存在实数k,k<0 ,使沿直线l把弧AD翻转后所得的弧与OA相切?
若存在,请求出此时k的值,若不存在,请说明理由。(6)分
[命题意图]圆在坐标系的变换情况
[参考答案]答案:如图所示,由
∠DEO=∠EAD+∠ADE=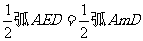 =∠AOD
=∠AOD
所以,OD=DE
当k=-2时,易得A(0,2),B(1,0),OA=2,OB=1,则AB=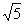
因为BO与⊙P切于点O,由切割线定理,得
OB2=BD·AB BD=
BD= 过点D作DC⊥AO于点C,则OE=2OC,DC∥OB 从而,有
过点D作DC⊥AO于点C,则OE=2OC,DC∥OB 从而,有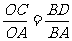
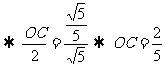 故OE=
故OE=
(2)假设存在实数k使得弧AD沿直线l翻转后所得弧与OA相切,则切点必为A,即E与A重合,由(1)知OD=AD。又∠ADO=90°,所以∠OAD=45°此时,OB=OA=2,B(2,0) ∴k=-1,
故存在k=-1,使得弧AD沿直l翻转后所得弧与OA相切。 (6)
[试题来源]2009北京中考模拟
26. .已知:抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
[命题意图]二次函数和一元二次方程根与系数关系
[参考答案]解:1)解方程x2-10x+16=0得x1=2,x2=8
∵点B在x轴的正半轴上,点C在y轴的正半轴上,且OB<OC
∴点B的坐标为(2,0),点C的坐标为(0,8)
又∵抛物线y=ax2+bx+c的对称轴是直线x=-2 ∴由抛物线的对称性可得点A的坐标为(-6,0)∴A、B、C三点的坐标分别是A(-6,0)、B(2,0)、C(0,8) (4分)
(2)∵点C(0,8)在抛物线y=ax2+bx+c的图象上
∴c=8,将A(-6,0)、B(2,0)代入表达式y=ax2+bx+8,得
∴所求抛物线的表达式为y=-x2-x+8
[试题来源]本校月考加工总结所得
25. (本题满分10分) 如图10,一次函数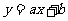 的图象与反比例函数
的图象与反比例函数 的图象交于M、N两点.
的图象交于M、N两点.
(1)求反比例函数和一次函数的解析式;
 (2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.
(2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.
[命题意图]一次函数和反比例函数的综合应用
[参考答案](1)将N( 1,
1, 4)代入
4)代入 中 得k=4
(2分)
中 得k=4
(2分)
反比例函数的解析式为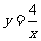
将M(2,m)代入解析式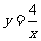 中 得m=2
(4
中 得m=2
(4
将M(2,2),N( 1,
1, 4)代入
4)代入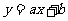 中
中
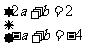 解得a=2 b=-2
(5分)一次函数解析式为
解得a=2 b=-2
(5分)一次函数解析式为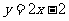
[试题来源]本校月考加工总结所得
24.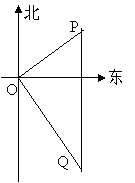 小明在某风景区的观景台O处观测到北偏东500的P处有一艘货船,该船正向南匀速航行,30分钟后再观察时,该船已航行到O的南偏东400,且与O相距2km的Q处.如图所示.
小明在某风景区的观景台O处观测到北偏东500的P处有一艘货船,该船正向南匀速航行,30分钟后再观察时,该船已航行到O的南偏东400,且与O相距2km的Q处.如图所示.
求: (1)∠OPQ和∠OQP的度数;
(2)货船的航行速度是多少km/h?(结果精确到0.1km/h, 已知sin500=cos500=0.7660,cos500=sin400=0.6428, tan500=1.1918,an400=0.8391, 供选用.)
[命题意图]三角函数综合应用
[参考答案]解:(1)∠OPQ=50°, ∠OQP=40° (2分)
(2) ∠POQ=180°-40°-50°=90°,在Rt△POQ中,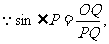
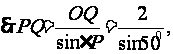
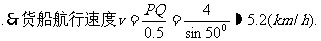
[试题来源]本校月考加工总结所得
23.(本题满分10分)新华商场为迎接家电下乡活动销售某种冰箱,每台进价为2500元,市场调研表明;当销售价定为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台,商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
[命题意图]考查学生对一元二次方程应用题的掌握情况
[参考答案]2750元
[试题来源]新海中学月考
22.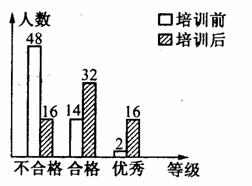 (本小题满分8分) 某校初三年级全体320名学生在一级B考试前后各参加了一次水平相同的考试,考分都以同一标准划分成“不及格”、“合格”、“优秀”三个等级,为了了解电脑培训的效果,用抽签方式得到其中64名学生的两次考试考分等级,所绘制的统计图如图所示,试结合图示信息回答下列问题:
(本小题满分8分) 某校初三年级全体320名学生在一级B考试前后各参加了一次水平相同的考试,考分都以同一标准划分成“不及格”、“合格”、“优秀”三个等级,为了了解电脑培训的效果,用抽签方式得到其中64名学生的两次考试考分等级,所绘制的统计图如图所示,试结合图示信息回答下列问题:
(1)这64名学生培训前考分的中位数所在的等级是 ;
(2)估计该校整个初三年级中,培训后考分等级为“优秀”的学生有 名;
(3)你认为上述估计合理吗?为什么?答: ,
理由: 。
[命题意图]统计知识的简单应用
[参考答案](1)不合格 (2)80名 (3)合理,理由,利用样本的优秀人数来诂计总体的优秀人数。
[试题来源]本校月考加工总结所得
20. (本小题满分8分)
如图,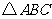 内接于
内接于 ,
, 为
为 的直径,
的直径,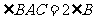 ,
,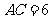 ,过点
,过点 作
作 的切线与
的切线与 的延长线交于点
的延长线交于点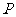 ,求
,求 的长.
的长.
[命题意图]特殊角三角函数和圆知识综合应用
[参考答案]解: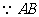 是
是 的直径,
的直径,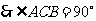 .又
.又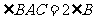 ,
,
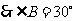 ,
,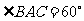 .
分
.
分
又 ,所以
,所以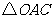 是等边三角形,由
是等边三角形,由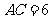 ,知
,知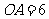 . 分
. 分
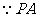 是
是 的切线,
的切线,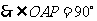 .
.
在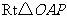 中,
中,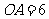 ,
,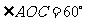 ,
,
所以,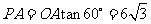 。
8[试题来源]新海中学模拟试题
。
8[试题来源]新海中学模拟试题
21(本小题满分8分)如图,已知四边形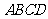 中,点
中,点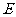 、
、 、
、 、
、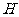 分别是
分别是 、
、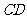 、
、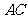 、
、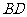 的中点,并且点
的中点,并且点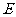 、
、 、
、 、
、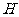 有在同一条直线上。
有在同一条直线上。
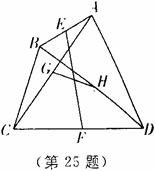 求证:
求证: 和
和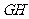 互相平分。
互相平分。
[命题意图]三角形中位线定理的应用和平行四边形的判断定理
[参考答案]连结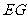 、
、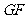 、
、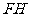 、
、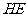 。点
。点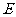 、
、 、
、 、
、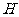 分别是
分别是 、
、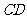 、
、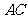 、
、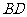 的中点。在
的中点。在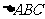 中,
中, ;在
;在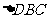 中,
中, ,
, 。
。 四边形
四边形 为平行四边形。
为平行四边形。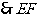 与
与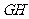 互相平分。
互相平分。
[试题来源]南京中考模拟试题
19. 已知正比例函数y=kx (k≠0)和反比例函数y=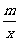 的图象都经过点(4,2).
的图象都经过点(4,2).
(1)求这两个函数的解析式.
(2)这两个函数图象还有其他交点吗?若有,请求出交点的坐标;若没有,请说明理由.
[命题意图]正比例函数和反比例函数的交点
[参考答案]解:(1)y=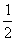 x, y=
x, y= (4分);(2)另一交点坐标为(-4,-2) (4分)
(4分);(2)另一交点坐标为(-4,-2) (4分)
[试题来源]中考指南
18..在2,3,4,5,x五个数据中,平均数是4,那么这组数据的方差是( )
[命题意图]考查学生的平均数和方差能力运算
[参考答案]2
[试题来源]北京中考数学模拟改编
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com