
5.下列运算中,结果正确的是 ( )
(A) (B)
(B) (C)
(C)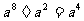 (D)
(D)
[命题意图]有理数的运算
[参考答案]B
[试题来源]九年级随堂练习改编
4. 已知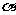 为锐角,且
为锐角,且 ,则
,则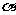 等于
等于
 A.
A.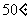 B.
B. C.
C. D.
D.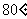
[命题意图]考查学生对三角函数的理解
[参考答案]C
[试题来源]天津模拟试题
3. 分式方程 的解是…………………………………………………………………………[ ]
的解是…………………………………………………………………………[ ]
A. x=1 B. x=-1 C. x=2 D. x=-2
[命题意图]考查分式方程的解法
[参考答案]A
[试题来源]中考指南
2. 2007年我省为135万名农村中小学生免费提供教科书,减轻了农民的负担,135万用科学计数法可表示为………………………………………………[ ]
A.0.135×106 B.1.35×106 C.0.135×107 D.1.35×107
[命题意图]联系生活实际,学生知道科学计数法
[参考答案]B
[试题来源]南京2008中考模拟试题
1. 下列多项式中,能用公式法分解因式的是…………………………………………………………[ ]
A.x2-xy B. x2+xy C. x2-y2 D. x2+y2
[命题意图]考察学生公式法分解因式的表示方法
[参考答案]C
[试题来源]天津2009中考模拟试题
2.如图,在平面直角坐标系中,矩形OABC的顶点A(0,3),C( ,0).将矩形OABC绕原点顺时针旋转90°,得到矩形
,0).将矩形OABC绕原点顺时针旋转90°,得到矩形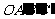 .设直线
.设直线 与
与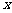 轴交于点M、与
轴交于点M、与 轴交于点N,抛物线
轴交于点N,抛物线 的图象经过点C、M、N.解答下列问题:
的图象经过点C、M、N.解答下列问题:
(1)分别求出直线 和抛物线所表示的函数解析式;
和抛物线所表示的函数解析式;
(2)将△MON沿直线MN翻折,点O落在点P处,请你判断点P是否在抛物线上,说明理由.
(3)将抛物线进行平移,使它经过点 ,求此时抛物线的解析式.
,求此时抛物线的解析式.
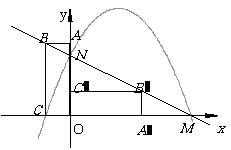
[命题意图]考查二次函数,图形翻折等综合应用能力,考查思维的深刻性
[参考答案](1)由题意得,B( ,3),
,3),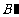 (3,1),∴直线
(3,1),∴直线 的解析式为
的解析式为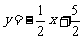 ;直线
;直线 与
与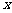 轴的交点为M(5,0),与
轴的交点为M(5,0),与 轴的交点N(0,
轴的交点N(0, ),设抛物线的解析式为
),设抛物线的解析式为 ,∵抛物线过点N,∴
,∵抛物线过点N,∴ ,∴
,∴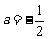 ,∴抛物线的解析式为
,∴抛物线的解析式为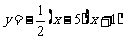 =
= ;
;
(2)将△MON沿直线MN翻折,点O落在点P处,则P为(2,4),点P不在抛物线上;
(3)若抛物线上下平移经过点 ,此时解析式为
,此时解析式为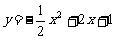 ;当
;当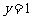 时
时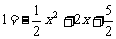 ,∴
,∴ ,
,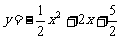 =
=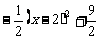 ,若抛物线向左平移经过点
,若抛物线向左平移经过点 ,平移距离为
,平移距离为 ,此时解析式为
,此时解析式为 =
= ;若抛物线向右平移经过点
;若抛物线向右平移经过点 ,此时解析式为
,此时解析式为
[试题来源]09年南京中考模拟试卷
1.已知点P是矩形ABCD边AB上的任意一点(与点A、B不重合)
(1)如图①,现将△PBC沿PC翻折得到△PEC;再在AD上取一点F,将△PAF沿PF翻折得到△PGF,并使得射线PE、PG重合,试问FG与CE的位置关系如何,请说明理由;
 (2)在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的大小关系,并说明你的理由;
(2)在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的大小关系,并说明你的理由;
(3)如图③,分别在AD、BC上取点F、C’,使得∠APF=∠BPC’,与(1)中的操作相类似,即将△PAF沿PF翻折得到△PFG,并将△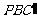 沿
沿 翻折得到△
翻折得到△ ,连接
,连接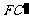 ,取
,取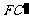 的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.
的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.
[命题意图]综合考查图形变换的性质,逻辑推理能力以及探究能力
[参考答案](1)FG∥CE,在矩形ABCD中,∠A=∠B=90°,由题意得,∠G=∠A=90°,∠PEC=∠B=90°,∴∠GEC=90°,∴∠G=∠GEC,∴FG∥CE。
(2)GH=EH。延长GH交CE于点M,由(1)得,FG∥CE,∴∠GFH=∠MCH,∵H为CF的中点,∴FH=CH,又∵∠GHF=∠MHC,∴△GFH≌△MHC,∴GH=HM=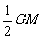 ,∵∠GEC=90°,∴EH=
,∵∠GEC=90°,∴EH= ,∴GH=EH。
,∴GH=EH。
(3)(2)中的结论还成立。取PF的中点M, 的中点N,∵∠FGP=90°,M为PF的中点,∴
的中点N,∵∠FGP=90°,M为PF的中点,∴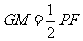 ,
, ,
, ∥
∥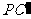 ,∴GM=PM,∴∠GPF=∠MGP,∴∠GMF=∠GPF+∠MGP=2∠GPF,∵H为
,∴GM=PM,∴∠GPF=∠MGP,∴∠GMF=∠GPF+∠MGP=2∠GPF,∵H为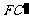 的中点,M为PF的中点,∴
的中点,M为PF的中点,∴ ,同理
,同理 ,
,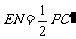 ,HN∥PF,∠
,HN∥PF,∠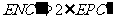 ,∴GM=HN,HM=EN。∵∠GPF=∠FPA,
,∴GM=HN,HM=EN。∵∠GPF=∠FPA, ,又
,又 ,∴∠GPF=
,∴∠GPF=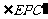 ,∴∠GMF=∠
,∴∠GMF=∠ ,∵
,∵ ∥
∥ ,HN∥PF,∴四边形HMPN为平行四边形,∴∠HMF=∠
,HN∥PF,∴四边形HMPN为平行四边形,∴∠HMF=∠ ,∴∠GMH=∠HNE,∵GM=HN,HM=EN,∴△GMH≌△HNE,∴GH=HE。
,∴∠GMH=∠HNE,∵GM=HN,HM=EN,∴△GMH≌△HNE,∴GH=HE。
[试题来源]09大丰中考模拟试卷
3.某工厂大楼后面紧邻着一个土坡,坡上面是一块平地,如图所示,BC∥AD,斜坡AB长22m,坡角∠BAD=600,为了防止山体滑坡,保障安全,工厂决定对该土坡进行改造.经地质人员勘测,当坡角不超过450时,可确保山体不滑坡.
(1)求改造前坡顶与地面的距离BE的长;
 (2)为确保安全,工厂计划改造时保持坡脚A不动,坡顶B沿BC削进到F点处,问BF至少是多少米?
(2)为确保安全,工厂计划改造时保持坡脚A不动,坡顶B沿BC削进到F点处,问BF至少是多少米?
[命题意图]考查三角函数的应用,问题呈现联系生活
[参考答案]解:(1)作BE⊥AD,E为垂足,则BE=AB·sin60°=22sin60°= (m).
(m).
(2)作FG⊥AD,G为垂足,连FA,
则FG=BE.∵AG=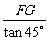 =
= ,
,
AE=AB·cos60°=22cos60°=11,
∴BF=AG-AE= (m),
(m),
即BF至少是 米.
米.
[试题来源]09江阴中考模拟试卷
1.将分别标有数字1,2,3的三张卡片洗匀后,背面朝上放在桌面上.
(1)随机地抽取一张,求P(抽到偶数);
(2)随机地抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,恰好这个两位数是奇数的概率是多少?
[命题意图]考查概率
[参考答案]解:(1)P(抽到偶数)=
(2)所有可能两位数列举如下:12,13,21,23,31,32
这个两位数是奇数的概率是
[试题来源]改编
2为减少环境污染,自2008年6月1日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分:
“限塑令”实施后,塑料购物袋使用后的处理方式统计表
|
处理方式 |
直接丢弃 |
直接做垃圾袋 |
再次购物使用 |
其它 |
|
选该项的人数占 总人数的百分比 |
5% |
35% |
49% |
11% |
请你根据以上信息解答下列问题:
(1)补全图1,“限塑令”实施前,如果每天约有2 000人次到该超市购物.根据这100位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?
(2)补全图2,并根据统计图和统计表说明,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响.
[命题意图]考查统计知识以及数学应用能力,解决实际问题能力
[参考答案]解:(1)补全图1见下图.·································································· 1分
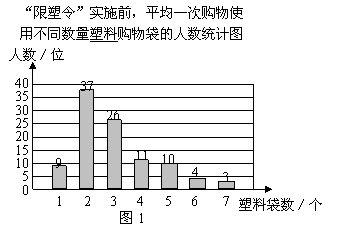
 (个).
(个).
这100位顾客平均一次购物使用塑料购物袋的平均数为3个.
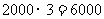 .
.
估计这个超市每天需要为顾客提供6000个塑料购物袋.
(2)图2中,使用收费塑料购物袋的人数所占百分比为 .
.
根据图表回答正确,例如:由图2和统计表可知,购物时应尽量使用自备袋和押金式环保袋,少用塑料购物袋;塑料购物袋应尽量循环使用,以便减少塑料购物袋的使用量,为环保做贡献.
[试题来源]重庆开县西街中学中考模拟
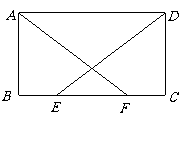
2.如图,在平行四边形ABCD中, 为
为 上两点,且
上两点,且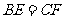 ,
,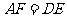 .
.
 求证:(1)
求证:(1)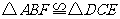 ;
;
(2)四边形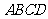 是矩形.
是矩形.
[命题意图]考查逻辑推理能力.
[参考答案](1)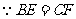 ,
,
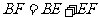 ,
,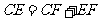 ,
,
 .
.  四边形
四边形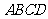 是平行四边形,
是平行四边形,
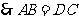 .
.
在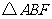 和
和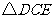 中,
中,
 ,
,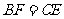 ,
,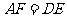 ,
,
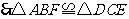 .
.
(2)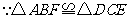 ,
,
 .
.  四边形
四边形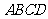 是平行四边形,
是平行四边形,
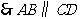 .
.
 .
.
 .
.
 四边形
四边形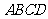 是矩形.
是矩形.
[试题来源]08南京中考试卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com