
例文1
河北 考生
社会不断发展,人民生活水平不断提高,但令不少父母担心的是自己的孩子是老师所谓的“坏孩子”。具体症状如下:思维活跃,看问题角度怪,立意新,且从不人云亦云,特别崇尚独立思
考。如一学生竟把“冰融化后变成什么”这一如此简单问题的答案写成“春天”,让人匪夷所思。本大学急家长之所急,想家长之所想,开办“坏孩子”大学,确保您的 孩子无论当初多么活跃,必将在毕业后成为人云亦云的顺民,成为适应时代需要的“人才”。
本大学特开办如下专业:
限制思维系。此乃我校热门专业,它会使您 的孩子思维僵化,毫无见解。毕业后可做秘书一类工作。该系教学特点如下:上课老师拼命灌,学生拼命记,作业如山题如海,只能听众老师意见,若有个人见解,即被老师罚站,倒立等等共“刑罚”36种。开始虽苦,日久天长定有飞跃,该系系主任:榆木头。
限制表达系。该系宗旨:纵有万语千言,绝不能吐露半点。该系学生特点:死板沉闷,属于“三棒子打不出一个屁”型。我系曾有一优秀毕业生,入学前风华正茂,时常指点江山,激扬文字,经过在该校的努力学习,终于沉默寡言。具体学习方法来校便知。系主任:哑吧。
此外本学校还有诸如限制运动系、限制交流系等。由于本校业绩突出,被誉为“制造顺民的大工厂”。该校环境死气沉沉,毫无生机,非常适合“坏孩子”学习。
鉴于知识经济的冲击,许多青年人思维异常活跃,以杨志远、李泽楷为榜样,使得学校生源日益减少。我校决定化压力为动力,决定减免部分优秀学生学费,以使本校事业发扬光大。
西谚云:“一千人看《哈姆雷特》,便有一千种不同见解。”在我校统统不适用。丰富多彩的答案在这里变成了固定死板的老师发的讲义。由于思维量大幅减少,必将使你心宽体胖,类似猪圈之中的“猪猡”。
欢迎广大无志青年报名。
报名时间:不限
报名地点:社会市普遍区现实路。
“坏孩子”大学招生办
即 日
简评:“答案是丰富多彩的”话题实质是倡导多角度思维和独立思考。本文作者却独辟蹊径,从反面切入,以介绍学校专业的方式,揭露 “应试教育”观念与体制束缚学生思维发展,禁锢学生个性、创造性等弊端与危害。全篇正话反说,幽默风趣,让读者在笑声中思考真理。
例文2
江苏 考生
本公司一向致力于市场急需产品的开发工作,通过对近两年有关权威市场调查数据报告的研究,我们发现:在高科技迅猛发展的今天,人与人之间的信任越来越少。而其根本原因就是人变得
不诚实了,更直接地说就是变得虚伪了。为了满足广大消费者渴求一个诚实守信社会到来的愿望,本公司竭力推出最新产品“诚信灵”。
21.(本小题满分14分)
已知函数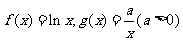 ,设
,设 。
。
(I)求函数 的单调区间;
的单调区间;
(Ⅱ)是否存在实数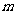 ,使得函数
,使得函数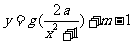 的图象与函数
的图象与函数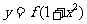 的图象恰有四个不同的交点?若存在,求出实数
的图象恰有四个不同的交点?若存在,求出实数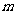 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
2009年度安徽六校教育研究会高二年级联考
20.(本小题满分13分)
如图,已知知线 与抛物线
与抛物线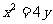 相切于点
相切于点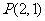 ,且与
,且与 轴交于点
轴交于点
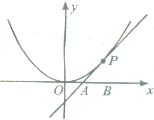
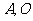 为坐标原点,定点
为坐标原点,定点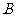 的坐标为(2,0)
的坐标为(2,0)
(I)若动点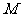 满足
满足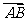
 ,求点
,求点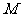 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)若过点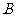 的直线
的直线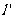 (斜率不等于零)与(I)中的轨迹
(斜率不等于零)与(I)中的轨迹 交于不同
交于不同
的两点 、
、 (
( 在
在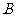 、
、 之间),试求
之间),试求 与
与 面积之比的
面积之比的
取值范围。
19.(本小题满分12分)
在长方体 中,
中,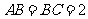 ,过
,过 、
、 、
、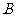 三点的平面截去
三点的平面截去
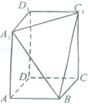 长方体的一个角后,得到如图所示的几何体
长方体的一个角后,得到如图所示的几何体 ,且这个几何体的体
,且这个几何体的体
积为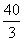 。
。
(I)求棱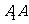 的长;
的长;
(Ⅱ)在线段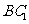 上是否存在点P,使直线
上是否存在点P,使直线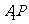 与
与 垂直,如果存在,求线段
垂直,如果存在,求线段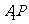 的长,如果不存在,请说明理由;
的长,如果不存在,请说明理由;
(Ⅲ)求平面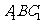 与平面
与平面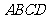 所成二面角的余弦值。
所成二面角的余弦值。
18.(本小题满分12分)
银河科技有限公司遇到一个技术难题,隧紧急成立甲、乙两个攻关小组,按要求各自独立进行为期一月的技术攻关,同时决定在攻关期满对攻克难题的小组给予奖励,已知这些技术难题在攻关期满时被甲小组攻克的概率为 ,被乙小组攻克的概率为
,被乙小组攻克的概率为 。
。
(I)设 为攻关期满时获奖小组的个数,求
为攻关期满时获奖小组的个数,求 的分布列及
的分布列及 ;
;
(Ⅱ)设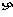 为攻关期满时获奖小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖小组数与没有获奖的攻关小组数之差的平方,记“函数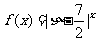 在定义域内单调递减“为事件
在定义域内单调递减“为事件 ,求事件
,求事件 发生的概率。
发生的概率。
17.(本小题满分12分)
已知数列 中,
中, 在直线
在直线 上,其中
上,其中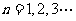
(I)令 求证数列
求证数列 是等比数列;
是等比数列;
(Ⅱ)求数列 的通项;
的通项;
(Ⅲ)设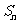 、
、 分别为数列
分别为数列 、
、 的前
的前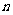 项和,是否存在实数
项和,是否存在实数 ,使得数列
,使得数列 为等差数列?若存在,是求出
为等差数列?若存在,是求出 的值;若不存在,则说明理由。
的值;若不存在,则说明理由。
16.(本小题满分12分)
已知 ,求
,求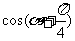 的值。
的值。
15.已知抛物线 的准线与双曲线
的准线与双曲线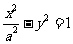 交于
交于 、
、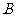 两点,点
两点,点 为抛物线的焦点,若△
为抛物线的焦点,若△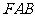 为直角三角形,则该双曲线的离心率是________________。
为直角三角形,则该双曲线的离心率是________________。
14.已知函数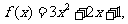 若
若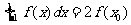 成立,则
成立,则 ___________。
___________。
13.已知等差数列 中,有
中,有 ,则在等比数列
,则在等比数列 中,会有类似的结论_____________。
中,会有类似的结论_____________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com